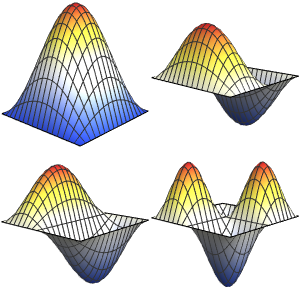
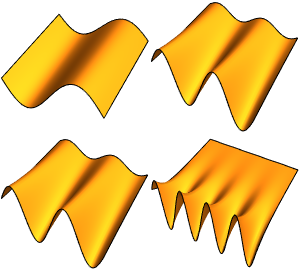
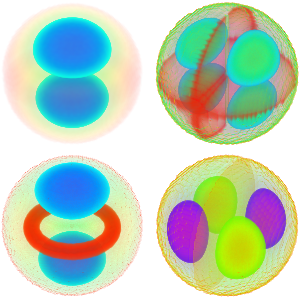
Compute Symbolic Eigenvalues
Specify a 1D Laplacian operator.
In[1]:=
\[ScriptCapitalL] = -Laplacian[u[x], {x}];Specify a homogeneous Dirichlet boundary condition.
In[2]:=
\[ScriptCapitalB] = DirichletCondition[u[x] == 0, True];Find expressions for the 5 smallest eigenvalues on the interval 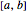 .
.
In[3]:=
DEigenvalues[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, a, b},
5]Out[3]=
Specify an Airy operator.
In[4]:=
\[ScriptCapitalL] = -Laplacian[u[x], {x}] + x u[x];Find the 5 smallest eigenvalues and corresponding eigenfunctions.
In[5]:=
{vals, funs} =
DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]},
u[x], {x, 0, 1}, 5];The eigenvalues are roots of a transcendental equation.
In[6]:=
vals[[1]] // TraditionalFormOut[6]//TraditionalForm=
Compute a transcendental eigenvalue with high precision.
In[7]:=
N[vals[[1]], 500] // TraditionalFormOut[7]//TraditionalForm=

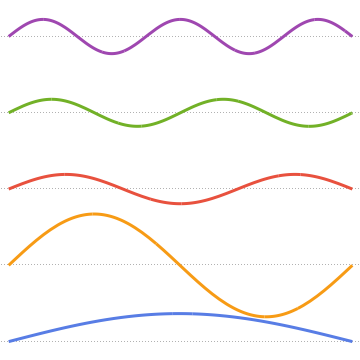
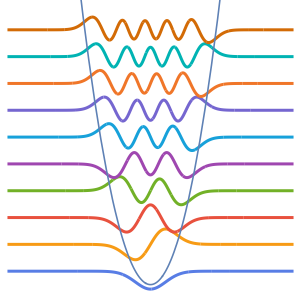
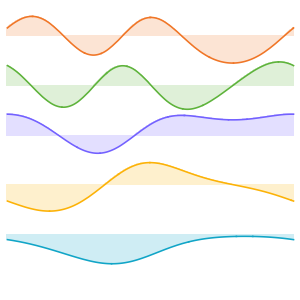
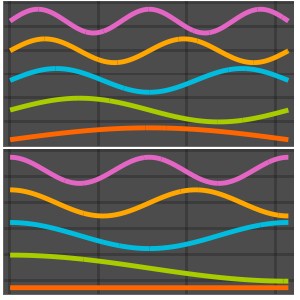
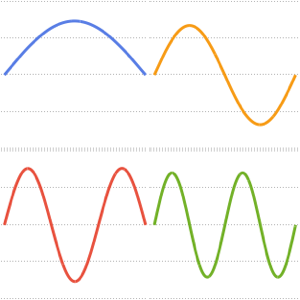
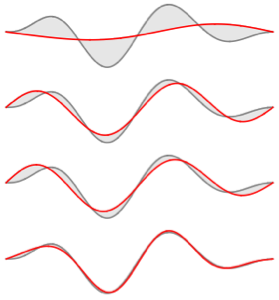
Visualize the eigenfunctions.
In[8]:=
Plot[Evaluate[funs + Range[5]], {x, 0, 1}, ImageSize -> Medium,
PlotTheme -> {"Business", "Bare"}, AspectRatio -> 1]Out[8]=