Find Aharonov–Bohm Eigenvalues
The Aharonov–Bohm effect is a quantum mechanical phenomenon where a charged particle detects an electromagnetic gauge potential even though the magnetic field inside the region where the particle can move is zero. In this example, the Schrödinger equation for a fixed magnetic field concentrated at a line perpendicular to the domain of the particle is considered.
Specify the region as sector in the 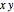 plane centered about the
plane centered about the 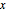 axis.
axis.
In[1]:=
\[CapitalOmega] = Disk[{0, 0}, 1, {-\[Pi]/8, \[Pi]/8}];Specify the Aharonov–Bohm operator. The magnetic field is restricted to the 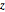 axis.
axis.
In[2]:=
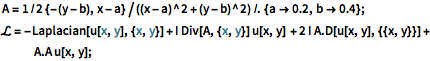
A = 1/2 {-(y - b), x - a}/((x - a)^2 + (y - b)^2) /. {a -> 0.2,
b -> 0.4};
\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}] +
I Div[A, {x, y}] u[x, y] + 2 I A.D[u[x, y], {{x, y}}] +
A.A u[x, y];Specify Dirichlet boundary conditions on the entire boundary.
In[3]:=
\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];Compute six eigenvalues and eigenfunctions of the operator.
In[4]:=
{vals, funs} =
NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]},
u[x, y], {x, y} \[Element] \[CapitalOmega], 6]; Inspect the eigenvalues.
In[5]:=
valsOut[5]=
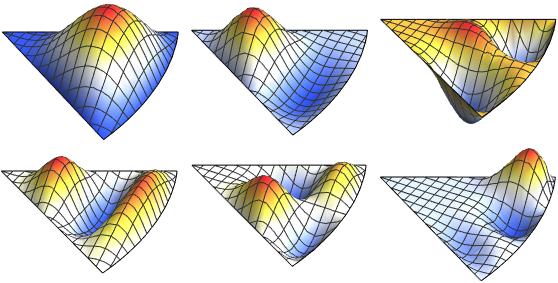
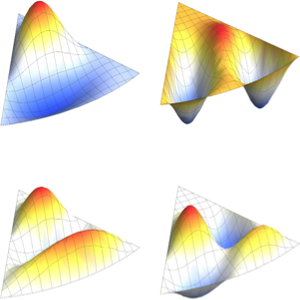
Visualize the real part of the eigenfunctions.
show complete Wolfram Language input
Out[6]=