求阿哈罗诺夫–玻姆特征值: Wolfram语言 11 的新功能

‹›

求阿哈罗诺夫–玻姆特征值

阿哈罗诺夫–玻姆效应是一种量子力学现象. 一个带电粒子可以探测到电磁规范势，即使在它运动的区域内磁场为零. 下面的例子考虑的是恒定磁场集中于一条垂直于粒子所处区域的直线上时的磁薛定谔方程.

在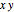平面设定以 X 轴为中心的一个扇面区域.

In[1]:=

\[CapitalOmega] = Disk[{0, 0}, 1, {-\[Pi]/8, \[Pi]/8}];

设定阿哈罗诺夫–玻姆算子. 磁场只局限于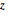轴.

In[2]:=

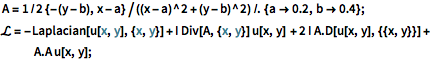
 A = 1/2 {-(y - b), x - a}/((x - a)^2 + (y - b)^2) /. {a -> 0.2, 
    b -> 0.4};
\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}] + 
   I Div[A, {x, y}] u[x, y] + 2 I A.D[u[x, y], {{x, y}}] + 
   A.A u[x, y];

在整个边界上设定狄利克雷边界条件.

In[3]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

计算该算子的六个特征值和特征函数.

In[4]:=

{vals, funs} = 
  NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, 
   u[x, y], {x, y} \[Element] \[CapitalOmega], 6];

查看特征值.

In[5]:=

vals

Out[5]=

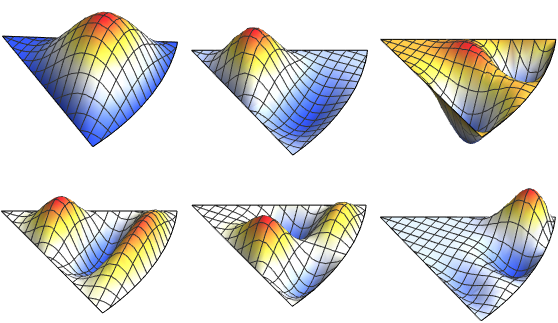
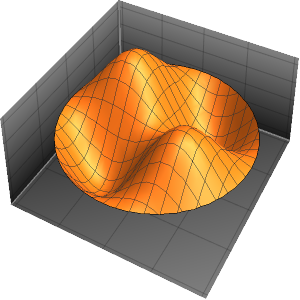
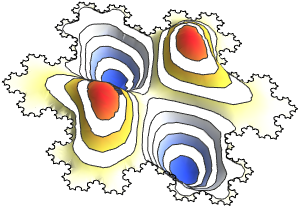
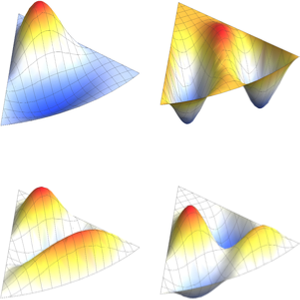
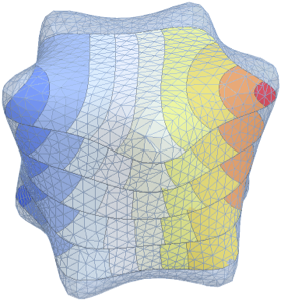
将特征函数的实部可视化.

显示完整的 Wolfram 语言输入

In[6]:=

Grid[Partition[
   Plot3D[Re[#], {x, y} \[Element] \[CapitalOmega], 
      ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None,
       PlotRange -> All, PlotStyle -> {Specularity[White, 20]}, 
      Method -> {"ShrinkWrap" -> True}] & /@ funs, 3], 
  Background -> Transparent] // Quiet

Out[6]=