アハラノフ・ボーム(Aharonov–Bohm)固有値を求める: Wolfram言語 11の新機能

アハラノフ・ボーム(Aharonov–Bohm)固有値を求める

アハラノフ・ボーム効果とは，粒子が動くことのできる範囲内部の磁場がゼロであっても，電荷を持つ粒子が電磁ゲージポテンシャルを検出する量子力学の現象である．この例では，粒子の領域に垂直な線に集中した固定磁場に対するシュレーディンガー(Schrödinger)方程式を考える．

領域を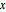，軸を中心とする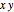平面の扇型として指定する．

In[1]:=

\[CapitalOmega] = Disk[{0, 0}, 1, {-\[Pi]/8, \[Pi]/8}];

アハラノフ・ボーム演算子を指定する．磁場は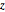軸に制限される．

In[2]:=

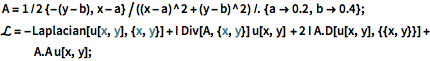
 A = 1/2 {-(y - b), x - a}/((x - a)^2 + (y - b)^2) /. {a -> 0.2, 
    b -> 0.4};
\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}] + 
   I Div[A, {x, y}] u[x, y] + 2 I A.D[u[x, y], {{x, y}}] + 
   A.A u[x, y];

境界全体についてディリクレ境界条件を指定する．

In[3]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

演算子の固有値と固有関数を6個計算する．

In[4]:=

{vals, funs} = 
  NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, 
   u[x, y], {x, y} \[Element] \[CapitalOmega], 6];

固有値を調べる．

In[5]:=

vals

Out[5]=

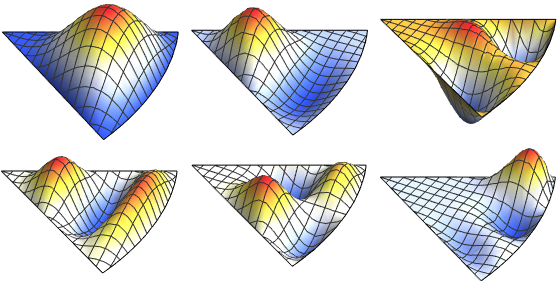
固有関数の実部を可視化する．

完全なWolfram言語入力を表示する

In[6]:=

Grid[Partition[
   Plot3D[Re[#], {x, y} \[Element] \[CapitalOmega], 
      ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None,
       PlotRange -> All, PlotStyle -> {Specularity[White, 20]}, 
      Method -> {"ShrinkWrap" -> True}] & /@ funs, 3], 
  Background -> Transparent] // Quiet

Out[6]=