Trouvez les valeurs propres d'Aharonov–Bohm: Nouveautés de Wolfram Language 11

Trouvez les valeurs propres d'Aharonov–Bohm

L'effet d'Aharonov–Bohm est un phénomène mécanique quantique où une particule chargée détecte un jauge électromagnétique potentiel, même si le champ magnétique à l'intérieur de la région où la particule peut se déplacer est zéro. Dans cet exemple, l'équation de Schrödinger pour un champ magnétique fixe concentré à une ligne perpendiculaire au domaine de la particule est considérée.

Précisez la région comme le secteur dans le plan 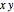x y centré autour de l'axe x.

In[1]:=

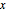\[CapitalOmega] = Disk[{0, 0}, 1, {-\[Pi]/8, \[Pi]/8}];

Précisez l'opérateur Aharonov-Bohm. Le champ magnétique est restreint à l'axe 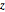z.

In[2]:=

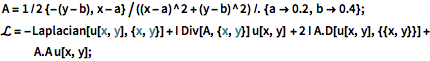
 A = 1/2 {-(y - b), x - a}/((x - a)^2 + (y - b)^2) /. {a -> 0.2, 
    b -> 0.4};
\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}] + 
   I Div[A, {x, y}] u[x, y] + 2 I A.D[u[x, y], {{x, y}}] + 
   A.A u[x, y];

Précisez les conditions aux limites de Dirichlet sur la frontière entière.

In[3]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

Calculez six valeurs et fonctions propres de l'opérateur.

In[4]:=

{vals, funs} = 
  NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, 
   u[x, y], {x, y} \[Element] \[CapitalOmega], 6];

Inspectez les valeurs propres.

In[5]:=

vals

Out[5]=

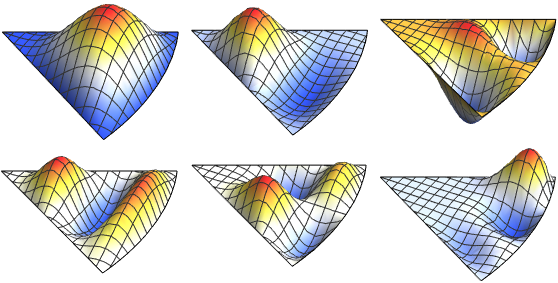
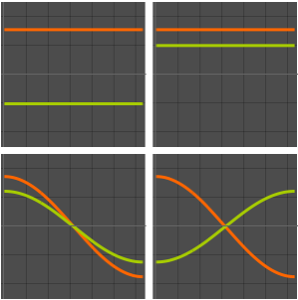
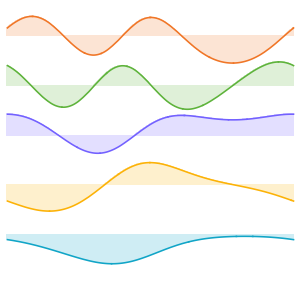
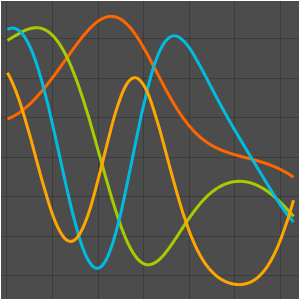
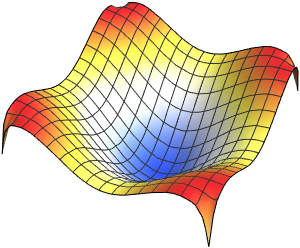
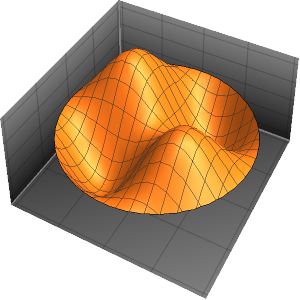
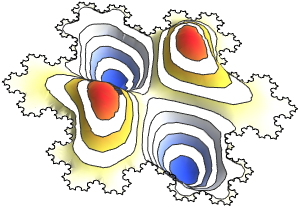
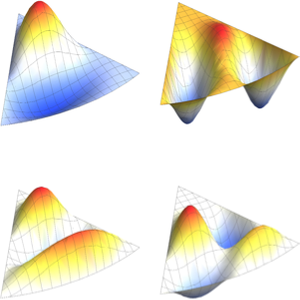
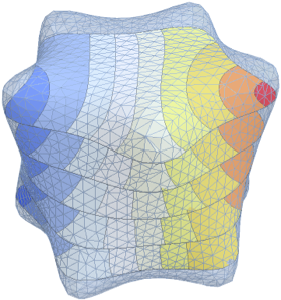
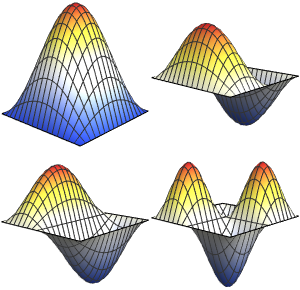
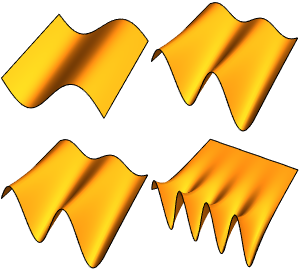
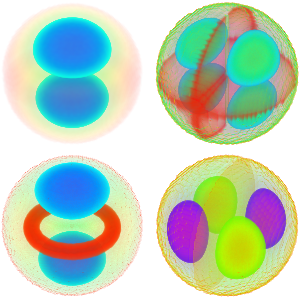
Visualisez la partie réelle des fonctions propres.

Montrer l'entrée complète de Wolfram Language

In[6]:=

Grid[Partition[
   Plot3D[Re[#], {x, y} \[Element] \[CapitalOmega], 
      ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None,
       PlotRange -> All, PlotStyle -> {Specularity[White, 20]}, 
      Method -> {"ShrinkWrap" -> True}] & /@ funs, 3], 
  Background -> Transparent] // Quiet

Out[6]=