Найти собственные значения Ахаронова-Бома: Новое в системе Wolfram Language 11

Найти собственные значения Ахаронова-Бома

Эффект Ахаранова-Бома представляет собой квантово-механическое явление, в котором заряженная частица обнаруживает электромагнитный калибровочный потенциал, даже если магнитное поле внутри области, где частица может двигаться, равнo нулю. В этом примере, мы рассмотрим уравнение Шредингера для фиксированного магнитного поля, сосредоточенного в линии, перпендикулярной домену частицы.

Укажем регион в качестве сектора в плоскости 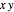с центром в районе оси .

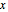In[1]:=

\[CapitalOmega] = Disk[{0, 0}, 1, {-\[Pi]/8, \[Pi]/8}];

Зададим оператор Ааронова-Бома. Магнитное поле ограничено осью .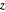

In[2]:=

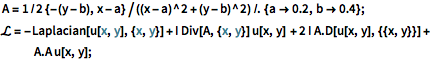
 A = 1/2 {-(y - b), x - a}/((x - a)^2 + (y - b)^2) /. {a -> 0.2, 
    b -> 0.4};
\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}] + 
   I Div[A, {x, y}] u[x, y] + 2 I A.D[u[x, y], {{x, y}}] + 
   A.A u[x, y];

Укажем граничные условия Дирихле по всей границе региона.

In[3]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

Рассчитаем шесть собственных значений и собственных функций оператора.

In[4]:=

{vals, funs} = 
  NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, 
   u[x, y], {x, y} \[Element] \[CapitalOmega], 6];

Проверим полученные собственные значения.

In[5]:=

vals

Out[5]=

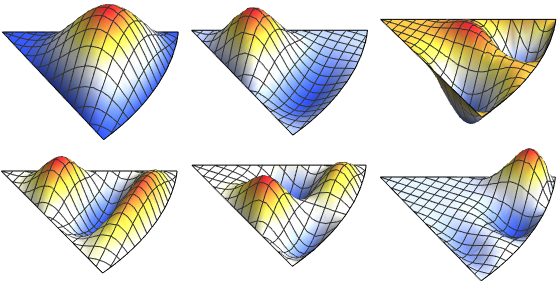
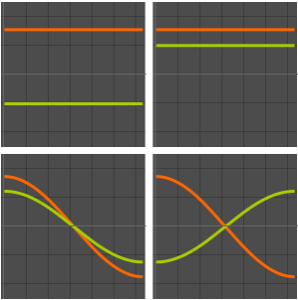
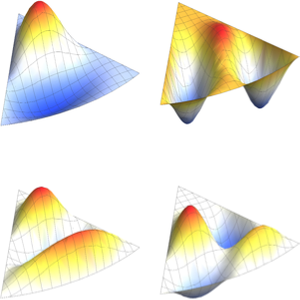
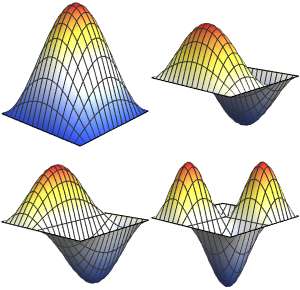
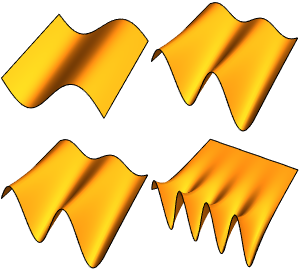
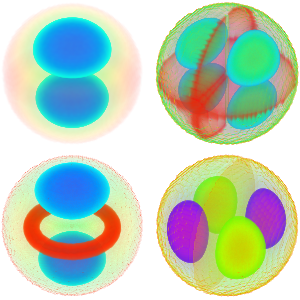
Визуализируем действительную часть собственных функций.

код на языке Wolfram Language целиком

In[6]:=

Grid[Partition[
   Plot3D[Re[#], {x, y} \[Element] \[CapitalOmega], 
      ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None,
       PlotRange -> All, PlotStyle -> {Specularity[White, 20]}, 
      Method -> {"ShrinkWrap" -> True}] & /@ funs, 3], 
  Background -> Transparent] // Quiet

Out[6]=