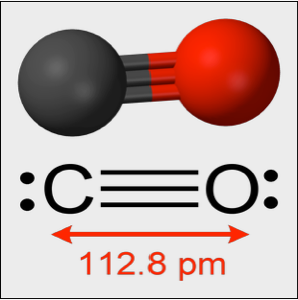
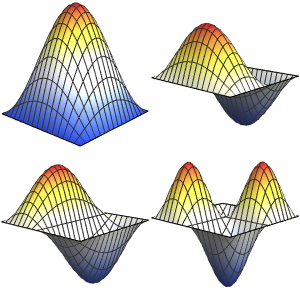
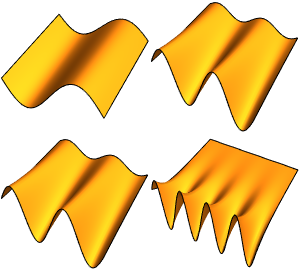
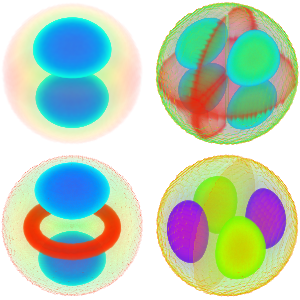
一酸化炭素分子の小さい振動をモデル化する
実験では，一酸化炭素分子は実質的なバネ定数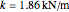 
で，その平衡位置の周りで振動する．振動は調和振動子方程式によって決定される．次では 
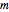は分子の換算質量，
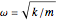は自然周波数，
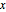は平衡位置からの移動，
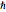は換算プランク(Planck)定数である．
In[1]:=
qho = -(\[HBar]^2/(2 m)) Laplacian[u[x], {x}] + (m \[Omega]^2)/
2 x^2 u[x];固有値および正規化された固有関数の最初の4個を計算する．
In[2]:=
sol = DEigensystem[qho, u[x], {x, -\[Infinity], \[Infinity]}, 4,
Assumptions -> \[HBar] > 0 && m > 0 && \[Omega] > 0,
Method -> "Normalize"]Out[2]=
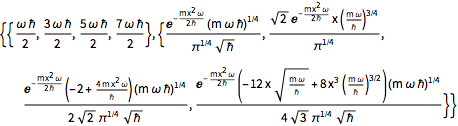
分子が4つの状態の等しい重ね合せになっていると仮定すると，波動関数の形は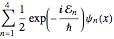
になる．
In[3]:=
\[Psi][x_, t_] = Total[MapThread[1/2 Exp[I E t #1/\[HBar]] #2 &, sol]]Out[3]=
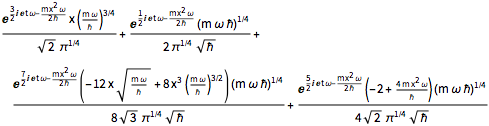
統一原子質量単位，フェムト秒，ピコメートルの基本単位を使って，3つのパラメータ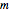 
，
，
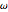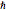を計算する．結果の値は1のオーダーに近付く．
In[4]:=
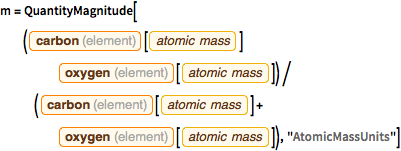
m = QuantityMagnitude[(
Entity["Element", "Carbon"][
EntityProperty["Element", "AtomicMass"]] Entity["Element",
"Oxygen"][EntityProperty["Element", "AtomicMass"]])/(
Entity["Element", "Carbon"][
EntityProperty["Element", "AtomicMass"]] +
Entity["Element", "Oxygen"][
EntityProperty["Element", "AtomicMass"]]), "AtomicMassUnits"]Out[4]=
In[5]:=
\[Omega] =
Sqrt[QuantityMagnitude[Quantity[1.86, "Kilonewtons"/"Meters"],
"AtomicMassUnit"/"Femtoseconds"^2]/m]Out[5]=
In[6]:=
\[HBar] =
QuantityMagnitude[Quantity[1., "ReducedPlanckConstant"],
"AtomicMassUnit"*"Picometers"^2/"Femtoseconds"]Out[6]=
移動の確率密度関数は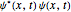 
で与えられる．
In[7]:=
\[Rho][x_, t_] =
FullSimplify[ComplexExpand[Conjugate[\[Psi][x, t]] \[Psi][x, t]]]Out[7]=
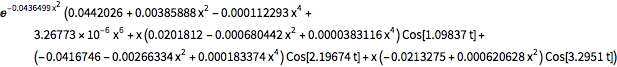
確率分布として，実数上の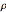 
の積分はすべての 
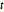に対して1である．
In[8]:=
Chop[Integrate[\[Rho][x, t], {x, -\[Infinity], \[Infinity]}]]Out[8]=
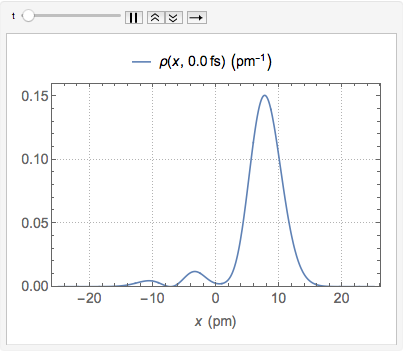
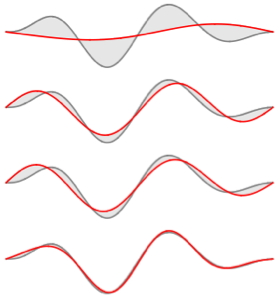
確率密度を経時的に可視化する．
完全なWolfram言語入力を表示する
