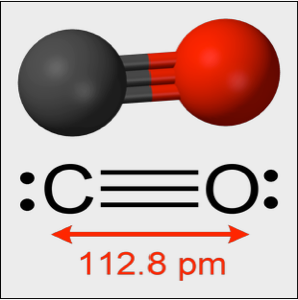
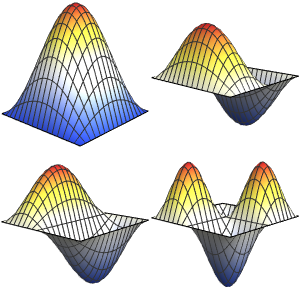
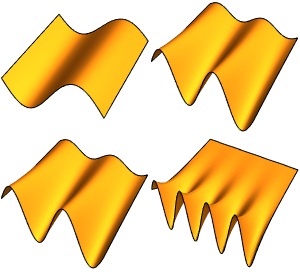
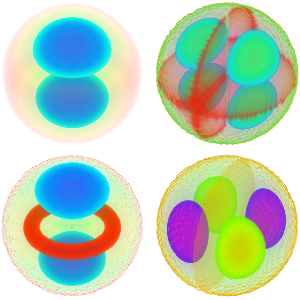
模拟 CO 分子上的小振动: Wolfram语言 11 的新功能

模拟 CO 分子上的小振动

从实验上看，一个 CO 分子会以有效弹性系数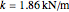在其平衡长度附近振动. 振动由量子简谐振子方程描述. 在下面的例子中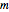，是分子的折合质量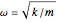，为固有频率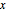，为相对平衡位置的位移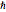，为约化普朗克常数.

In[1]:=

qho = -(\[HBar]^2/(2 m)) Laplacian[u[x], {x}] + (m \[Omega]^2)/
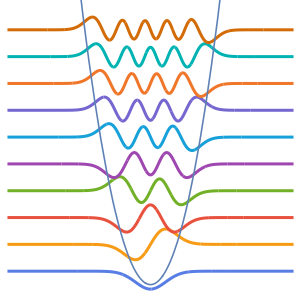
    2 x^2 u[x];

计算前四个特征值和归一化特征函数.

In[2]:=

sol = DEigensystem[qho, u[x], {x, -\[Infinity], \[Infinity]}, 4, 
  Assumptions -> \[HBar] > 0 && m > 0 && \[Omega] > 0, 
  Method -> "Normalize"]

Out[2]=

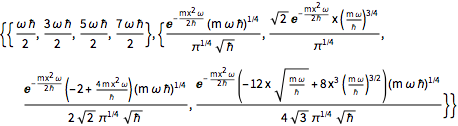
假定粒子处于四个态的等量叠加，则波函数将有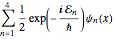的形式.

In[3]:=

\[Psi][x_, t_] = Total[MapThread[1/2 Exp[I E t #1/\[HBar]] #2 &, sol]]

Out[3]=

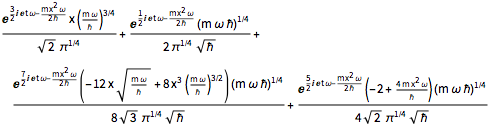
用原子质量单位、飞秒和皮米等基本单位来计算三个常数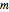、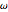和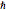，这样计算的值将接近 1 的量级.

In[4]:=

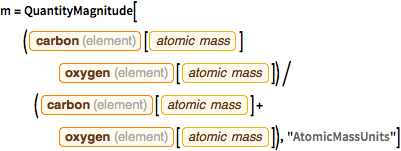
m = QuantityMagnitude[(
  Entity["Element", "Carbon"][
    EntityProperty["Element", "AtomicMass"]] Entity["Element", 
     "Oxygen"][EntityProperty["Element", "AtomicMass"]])/(
  Entity["Element", "Carbon"][
    EntityProperty["Element", "AtomicMass"]] + 
   Entity["Element", "Oxygen"][
    EntityProperty["Element", "AtomicMass"]]), "AtomicMassUnits"]

Out[4]=

In[5]:=

\[Omega] = 
 Sqrt[QuantityMagnitude[Quantity[1.86, "Kilonewtons"/"Meters"], 
    "AtomicMassUnit"/"Femtoseconds"^2]/m]

Out[5]=

In[6]:=

\[HBar] = 
 QuantityMagnitude[Quantity[1., "ReducedPlanckConstant"], 
  "AtomicMassUnit"*"Picometers"^2/"Femtoseconds"]

Out[6]=

位移概率密度函数由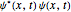给出.

In[7]:=

\[Rho][x_, t_] = 
 FullSimplify[ComplexExpand[Conjugate[\[Psi][x, t]] \[Psi][x, t]]]

Out[7]=

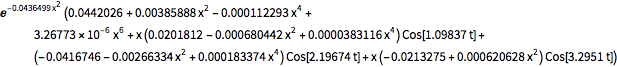
由于是概率分布，对所有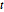，ρ 在实数上的积分都为 1.

In[8]:=

Chop[Integrate[\[Rho][x, t], {x, -\[Infinity], \[Infinity]}]]

Out[8]=

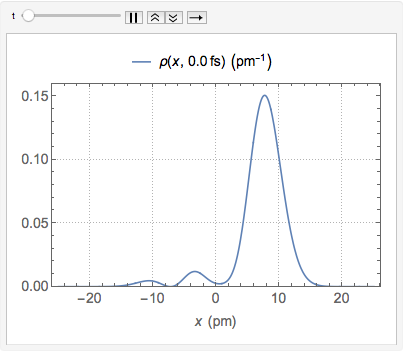
可视化概率密度随时间变化的情况.

显示完整的 Wolfram 语言输入

In[9]:=

Animate[Plot[\[Rho][x, t], {x, -25, 25}, PlotRange -> {0, .16}, 
  PlotTheme -> "Detailed", 
  FrameLabel -> {Row[{x, RawBoxes@RowBox[{"(", "\"pm\"", ")"}]}, 
     "  "], None}, LabelStyle -> Larger, 
  PlotLegends -> 
   Placed[{Row[{HoldForm[\[Rho]][x, 
        Quantity[NumberForm[t, {2, 1}], "Femtoseconds"]], 
       RawBoxes@RowBox[{"(", SuperscriptBox["\"pm\"", -1], ")"}]}, 
      "  "]}, Above]], {t, 0., 5.7, ImageSize -> Small}, 
 AnimationRate -> 1, SaveDefinitions -> True, Alignment -> Center]