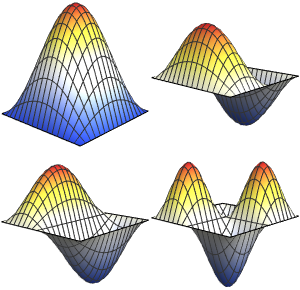
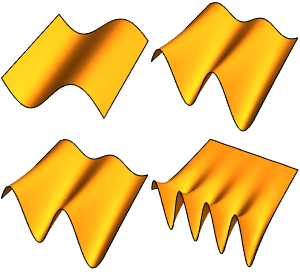
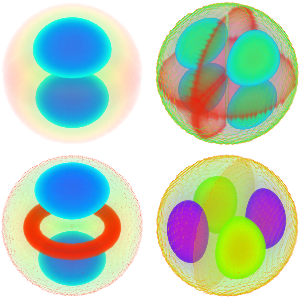
일산화탄소 분자의 작은 진동 모델화
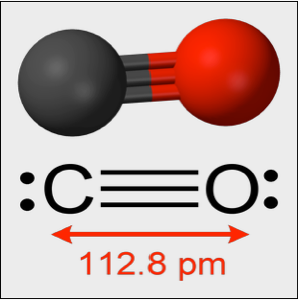
실험에서 일산화탄소 분자는 실질적인 스프링 상수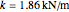 
를 가진 평형 길이 정도로 진동합니다. 진동은 양자 조화 진동 방정식에 의해 결정됩니다. 다음에서 
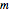은 환원 분자 질량, 
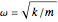은 자연 주파수, 
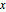는 평형 위치에서의 이동, 
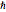는 환산 플랑크 상수를 의미합니다.
In[1]:=
qho = -(\[HBar]^2/(2 m)) Laplacian[u[x], {x}] + (m \[Omega]^2)/
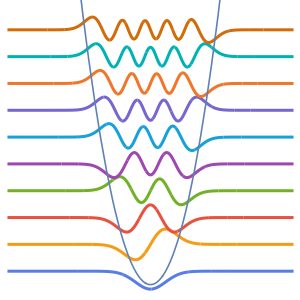
2 x^2 u[x];고유값 및 정규화 된 고유 함수의 첫 4개를 계산합니다.
In[2]:=
sol = DEigensystem[qho, u[x], {x, -\[Infinity], \[Infinity]}, 4,
Assumptions -> \[HBar] > 0 && m > 0 && \[Omega] > 0,
Method -> "Normalize"]Out[2]=
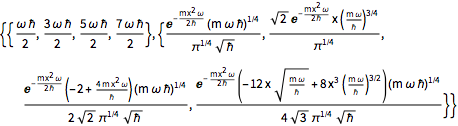
분자가 4개의 상태에 동일하게 중첩되어 있다고 가정하면 파동 함수는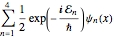 
형식을 얻습니다.
In[3]:=
\[Psi][x_, t_] = Total[MapThread[1/2 Exp[I E t #1/\[HBar]] #2 &, sol]]Out[3]=
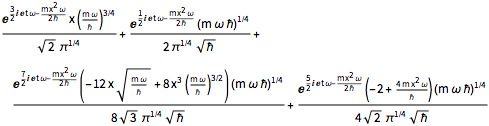
원자 질량 단위 펨토 세컨드, 피코미터의 기본 단위를 사용하여 3개의 매개 변수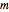 
, 
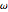, 그리고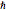 
을 계산하며 결과 값은 오더 유닛에 근접합니다.
In[4]:=
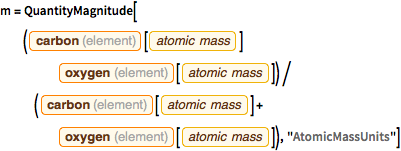
m = QuantityMagnitude[(
Entity["Element", "Carbon"][
EntityProperty["Element", "AtomicMass"]] Entity["Element",
"Oxygen"][EntityProperty["Element", "AtomicMass"]])/(
Entity["Element", "Carbon"][
EntityProperty["Element", "AtomicMass"]] +
Entity["Element", "Oxygen"][
EntityProperty["Element", "AtomicMass"]]), "AtomicMassUnits"]Out[4]=
In[5]:=
\[Omega] =
Sqrt[QuantityMagnitude[Quantity[1.86, "Kilonewtons"/"Meters"],
"AtomicMassUnit"/"Femtoseconds"^2]/m]Out[5]=
In[6]:=
\[HBar] =
QuantityMagnitude[Quantity[1., "ReducedPlanckConstant"],
"AtomicMassUnit"*"Picometers"^2/"Femtoseconds"]Out[6]=
이동의 확률 밀도 함수는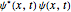 
로 주어집니다.
In[7]:=
\[Rho][x_, t_] =
FullSimplify[ComplexExpand[Conjugate[\[Psi][x, t]] \[Psi][x, t]]]Out[7]=
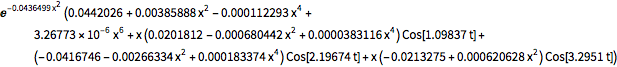
확률 분포로 실수의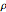 
적분은 모든 
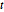에 대해 1입니다.
In[8]:=
Chop[Integrate[\[Rho][x, t], {x, -\[Infinity], \[Infinity]}]]Out[8]=
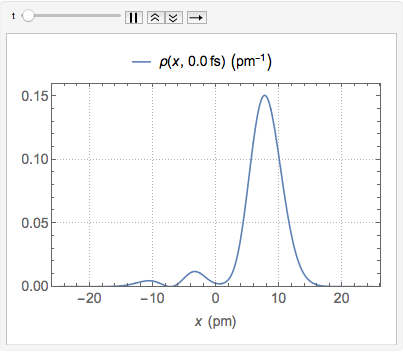
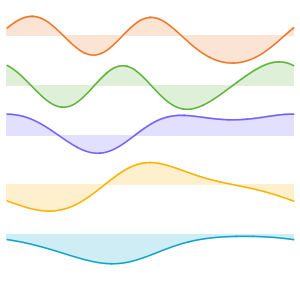
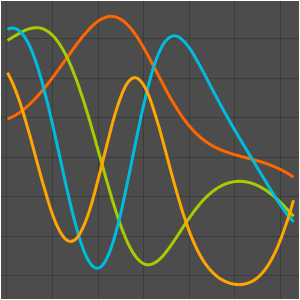
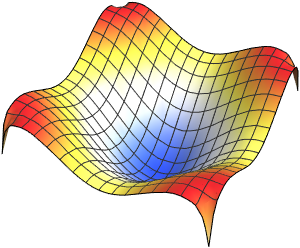
확률 밀도를 경시적으로 시각화합니다.
전체 Wolfram 언어 입력 표시하기
