Wolfram Mathematica

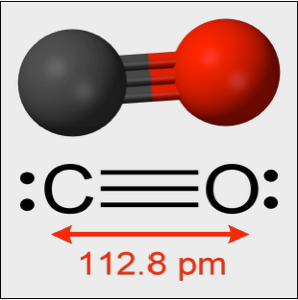
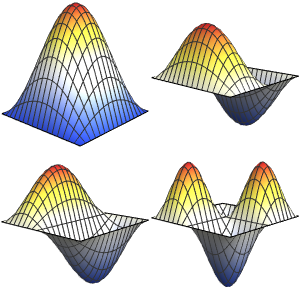
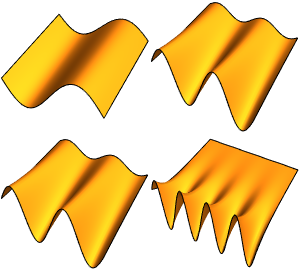
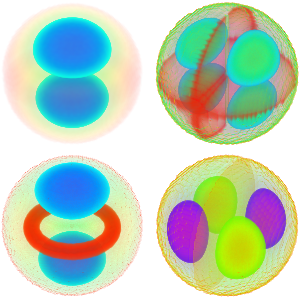
Model Small Oscillations in a CO Molecule

Experimentally, a CO molecule oscillates about its equilibrium length with an effective spring constant of 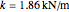. The oscillations are governed by the quantum harmonic oscillator equation. In the following, 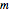is the reduced mass of the molecule, 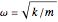is the natural frequency, 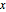is the displacement from the equilibrium position, and 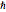is the reduced Planck's constant.

In[1]:=

qho = -(\[HBar]^2/(2 m)) Laplacian[u[x], {x}] + (m \[Omega]^2)/ 2 x^2 u[x];

Compute the first four eigenvalues and normalized eigenfunctions.

In[2]:=

sol = DEigensystem[qho, u[x], {x, -\[Infinity], \[Infinity]}, 4, Assumptions -> \[HBar] > 0 && m > 0 && \[Omega] > 0, Method -> "Normalize"]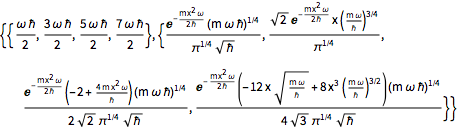

Out[2]=

Assuming the particle is in an equal superposition of the four states, the wavefunction will have the form .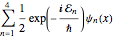

In[3]:=

\[Psi][x_, t_] = Total[MapThread[1/2 Exp[I E t #1/\[HBar]] #2 &, sol]]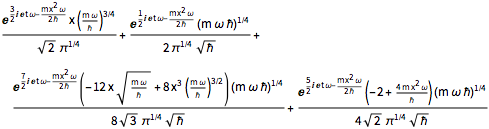

Out[3]=

Compute the three parameters , , 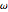and 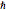using base units of atomic mass units, femtoseconds, and picometers, as the resulting values will be close to order unity.

In[4]:=

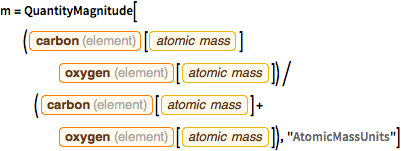
m = QuantityMagnitude[( Entity["Element", "Carbon"][ EntityProperty["Element", "AtomicMass"]] Entity["Element", "Oxygen"][EntityProperty["Element", "AtomicMass"]])/( Entity["Element", "Carbon"][ EntityProperty["Element", "AtomicMass"]] + Entity["Element", "Oxygen"][ EntityProperty["Element", "AtomicMass"]]), "AtomicMassUnits"]

Out[4]=

In[5]:=

\[Omega] = Sqrt[QuantityMagnitude[Quantity[1.86, "Kilonewtons"/"Meters"], "AtomicMassUnit"/"Femtoseconds"^2]/m]

Out[5]=

In[6]:=

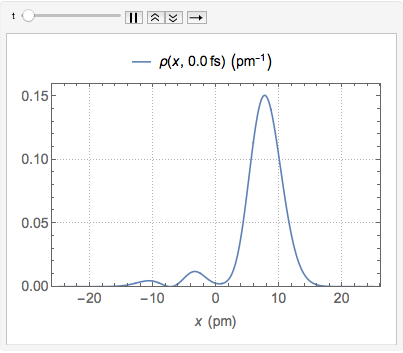
\[HBar] = QuantityMagnitude[Quantity[1., "ReducedPlanckConstant"], "AtomicMassUnit"*"Picometers"^2/"Femtoseconds"]

Out[6]=

The probability density function of the displacement is given by .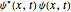

In[7]:=

\[Rho][x_, t_] = FullSimplify[ComplexExpand[Conjugate[\[Psi][x, t]] \[Psi][x, t]]]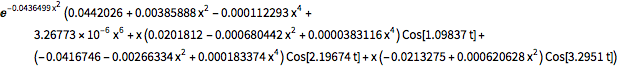

Out[7]=

As a probability distribution, the integral of 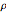over the reals is 1 for all .

In[8]:=

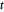Chop[Integrate[\[Rho][x, t], {x, -\[Infinity], \[Infinity]}]]

Out[8]=

Visualize the probability density over time.

In[9]:=

Animate[Plot[\[Rho][x, t], {x, -25, 25}, PlotRange -> {0, .16}, PlotTheme -> "Detailed", FrameLabel -> {Row[{x, RawBoxes@RowBox[{"(", "\"pm\"", ")"}]}, " "], None}, LabelStyle -> Larger, PlotLegends -> Placed[{Row[{HoldForm[\[Rho]][x, Quantity[NumberForm[t, {2, 1}], "Femtoseconds"]], RawBoxes@RowBox[{"(", SuperscriptBox["\"pm\"", -1], ")"}]}, " "]}, Above]], {t, 0., 5.7, ImageSize -> Small}, AnimationRate -> 1, SaveDefinitions -> True, Alignment -> Center]

Play Animation

Stop Animation