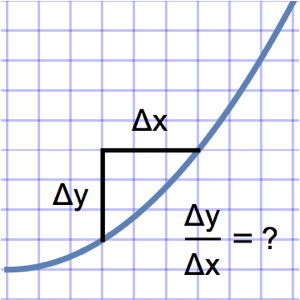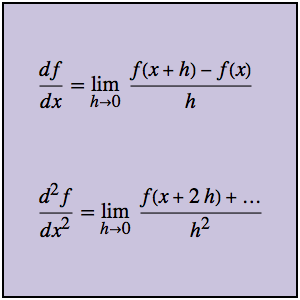Evaluate a Derivative Using First Principles
Difference quotients can be used directly to compute not only the first derivative, but higher-order derivatives as well. Consider first the function g and its associated difference quotient.
In[1]:=
g[x_] := x^2 Exp[x]In[2]:=
dq1[x_] = DifferenceQuotient[g[x], {x, h}]Out[2]=
Taking the limit of the difference quotient gives the first derivative.
In[3]:=
Limit[dq1[x], h -> 0]Out[3]=
In[4]:=
Limit[dq1[x], h -> 0];
Simplify[% == g'[x]]Out[4]=
The second derivative can be computed directly from the second difference quotient, without ever referencing the first derivative.
In[5]:=
dq2[x_] = DifferenceQuotient[g[x], {x, 2, h}]Out[5]=
The limit as 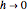 is the second derivative.
is the second derivative.
In[6]:=
Limit[dq2[x], h -> 0]Out[6]=
In[7]:=
Limit[dq2[x], h -> 0];
Simplify[% == g''[x]]Out[7]=
The difference quotient of the first derivative is a different function from the second-order difference quotient of g, but its limit is also the second derivative.
In[8]:=
dqp[x_] = DifferenceQuotient[g'[x], {x, h}]Out[8]=
In[9]:=
Limit[dqp[x], h -> 0]Out[9]=