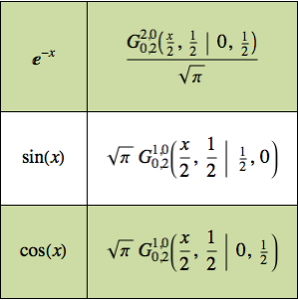Решение задачи с начальными условиями с использованием функции Грина
Решить задачу с начальными условиями для неоднородного дифференциального уравнения, используя функцию GreenFunction.
Начать с решения Грина.
In[1]:=
gf[s_, t_] =
GreenFunction[{-u''[t] + u'[t] - 37/4 u[t], u[0] == 0, u'[0] == 0},
u[t], {t, 0, \[Infinity]}, s]Out[1]=
Определить вынуждающую функцию.
In[2]:=
f[t_] := Cos[a t]Объединениe функции Грина с вынуждающей функцией приводит к решению.
In[3]:=
sol = Integrate[gf[s, t] f[s], {s, 0, \[Infinity]},
Assumptions -> t > 0]Out[3]=
Сравнить данный результат с результатом применения функции DSolveValue.
In[4]:=
DSolveValue[{-u''[t] + u'[t] - 37/4 u[t] == f[t], u[0] == 0,
u'[0] == 0}, u[t], t] // FullSimplifyOut[4]=
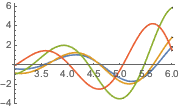
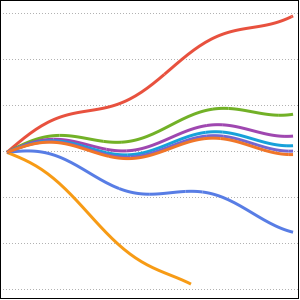
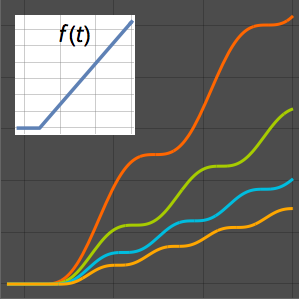
Отобразить решение данной задачи для разных значений параметра a.
In[5]:=
Plot[Table[sol, {a, 1, 4, 0.8}] // Evaluate, {t, 3, 6}]Out[5]=