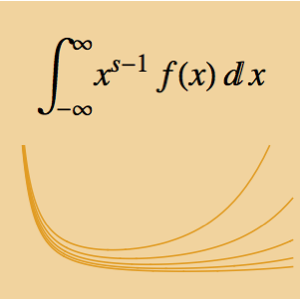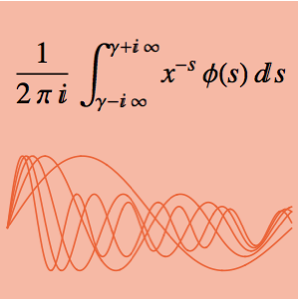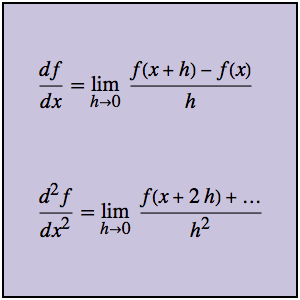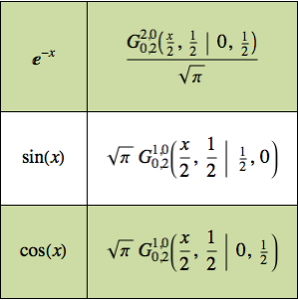Решить задачy общества промышленной и прикладной математики

Интеграл 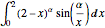зависит от параметра α. Найти значение α, находящеeся между 0 и 5 и увеличить интеграл до максимума. Заданный интеграл является свёрткой Меллина двух функций.

In[1]:=

f[x_] := x (2 - x)^\[Alpha] UnitBox[(x - 1)/2]

In[2]:=

g[x_] := Sin[x]

Вычислить свёртку Меллина для f[x] и g[x].

In[3]:=

(mc = MellinConvolve[f[x], g[x], x, \[Alpha]]) // TraditionalForm

Out[3]//TraditionalForm=

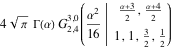
Сравнить с результатами, полученными от Integrate.

In[4]:=

Integrate[(2 - x)^\[Alpha] Sin[\[Alpha]/x], {x, 0, 2}, Assumptions -> \[Alpha] > 0] // TraditionalForm

Out[4]//TraditionalForm=

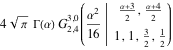
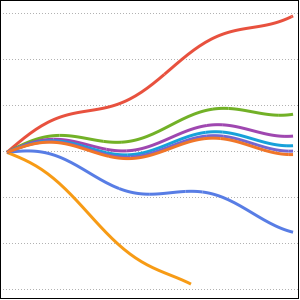
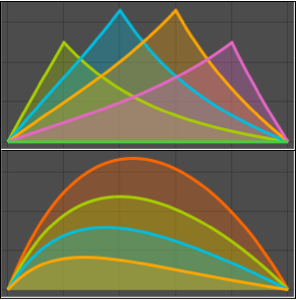
Графически отобразить интеграл функции α.

In[5]:=

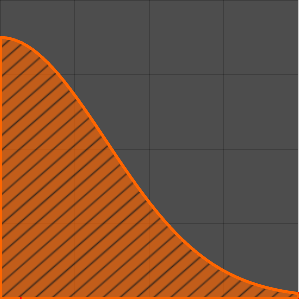
Plot[mc // Evaluate, {\[Alpha], 0, 4.99}, PlotStyle -> Red]

Out[5]=

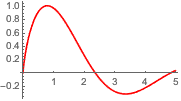
Вычислить независимую переменную, увеличивающую интеграл до максимума при 0≤α≤5, используя FindArgMax.

In[6]:=

N[FindArgMax[mc, {\[Alpha], 1}, WorkingPrecision -> 100][[1]], 20]

Out[6]=