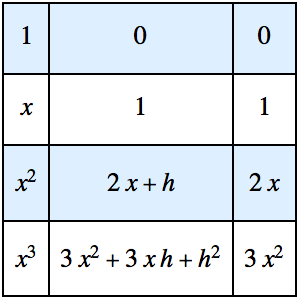
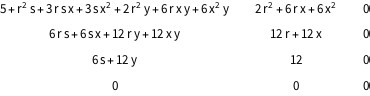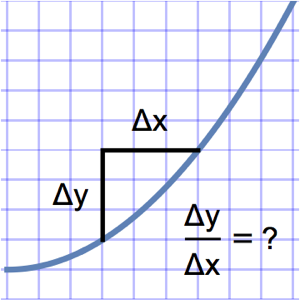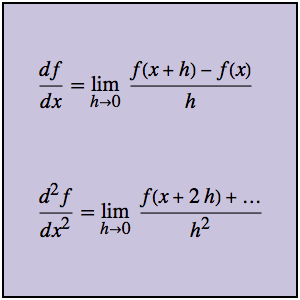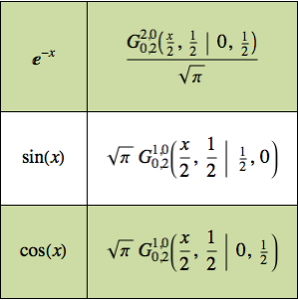Вычисление отношения разностей

Wolfram Language позволяет вычислять не только хорошо известные одномерные отношения разностей, но также многомерные производные и производные более высокого порядка.

In[1]:=

DifferenceQuotient[f[x], {x, h}]

Out[1]=

Отношение разностей второго порядка - это отношение разностей производной первого порядка.

In[2]:=

DifferenceQuotient[f[x], {x, 2, h}]

Out[2]=

In[3]:=

DifferenceQuotient[f[x], {x, h}]; DifferenceQuotient[f[x], {x, 2, h}]; % == DifferenceQuotient[%%, {x, h}]

Out[3]=

Вычислить многомерное отношение разностей.

In[4]:=

DifferenceQuotient[(x + y + 1)/(((x^2 + 3) (y + 5))), {x, h}, {y, k}]

Out[4]=

Создать таблицу возрастающих отношений разностей многочлена, которая представит многочлены в убывающем порядке.

In[5]:=

Grid[Table[ DifferenceQuotient[x^3 y^2 + 5 x y + 11, {x, i, r}, {y, j, s}], {i, 4}, {j, 3}], Spacings -> {2, 1}]

Out[5]=