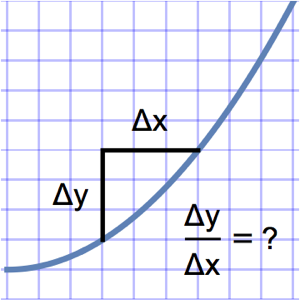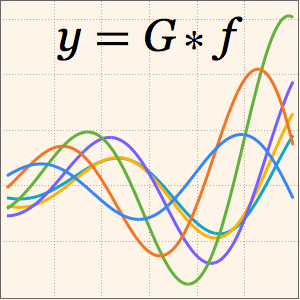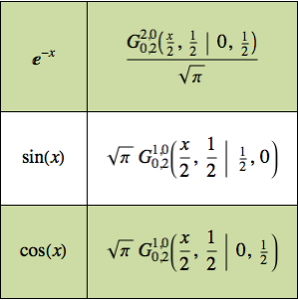Нахождение импульсионного сигнала цепи

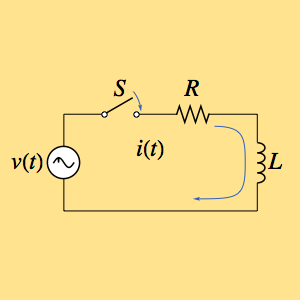
Найти импульсионный сигнал цепи, которая состоит из резистора 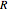и индуктора 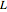и находится под напряжением 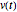, зависящем от времени.

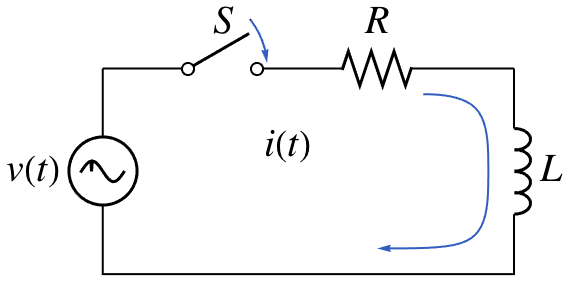
Текущее значение 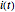может быть вычисленo путём решения линейного дифференциального уравнения первого порядка .

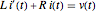Установить дифференциальный оператор в соответствии с левой частью обыкновенного дифференциального уравнения.

In[1]:=

voltage = L i'[t] + R i[t];

Допустим, что ключ изначально разомкнут.

In[2]:=

init = i[0] == 0;

Вычислить импульсионный сигнал для цепи, используя функцию GreenFunction.

In[3]:=

gf[s_, t_] = GreenFunction[{voltage, init}, i[t], {t, 0, \[Infinity]}, s]

Out[3]=

Отобразить на графике импульсионный сигнал при .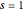

In[4]:=

Plot[gf[s, t] /. {s -> 1, R -> 2, L -> 4}, {t, 0, 7}, PlotTheme -> "Scientific", AxesLabel -> {"t", "i[t]"}]

Out[4]=

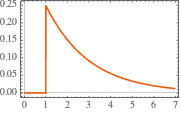
Вычислить сигнал цепи при ступенчатом изменении напряжения.

In[5]:=

v[t_] := HeavisideTheta[t];

In[6]:=

current = Integrate[gf[s, t] v[s], {s, 0, t}, Assumptions -> t > 0]

Out[6]=

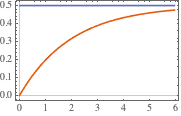
Визуализировать сигнал при ступенчатом изменении.

In[7]:=

Plot[{current /. {R -> 2, L -> 4}, 0.5} // Evaluate, {t, 0, 6}, PlotTheme -> "Scientific"]

Out[7]=