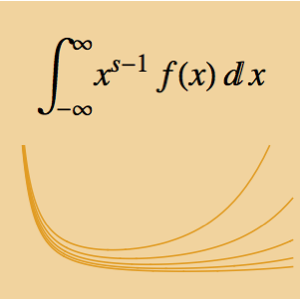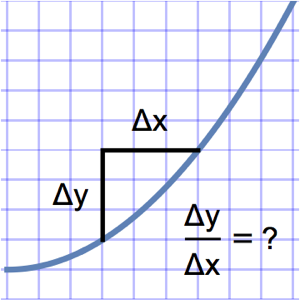Решение задачи о таутохроне
Задача о таутохроне требует нахождения определённой кривой. Если разместить бусину в любой точке данной кривой, то она упадёт на дно за одинаковый отрезок времени. Если выразить общее время падения через длину арки кривой, а скорость через v, то получим интегральное уравнение Абеля 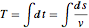 . Если выразить неизвестную функцию
. Если выразить неизвестную функцию 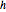 через отношение
через отношение 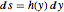 и использовать уравнение сохранения энергии
и использовать уравнение сохранения энергии 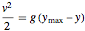 , то получим следующее уравнение.
, то получим следующее уравнение.
abeleqn = T == 1/Sqrt[2 g] \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(y\)]\(
\*FractionBox[\(h[z]\),
SqrtBox[\(y - z\)]] \[DifferentialD]z\)\);Решить интегральное уравнение с помощью функции DSolveValue.
dsdy = DSolveValue[abeleqn, h[y], y]Используя отношение 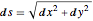 , найти решение для
, найти решение для 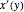 .
.
dxdy = Sqrt[dsdy^2 - 1]Начиная от края кривой, интегрировать 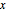 как функцию
как функцию 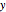 . Предположения обеспечивают вещественность подынтегрального уравнения.
. Предположения обеспечивают вещественность подынтегрального уравнения.
x[y_] = Integrate[dxdy, {y, 0, y},
Assumptions -> (2 g (T^2) )/(\[Pi]^2 y) > 1 && y > 0]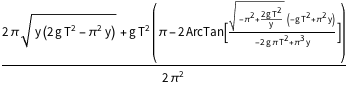
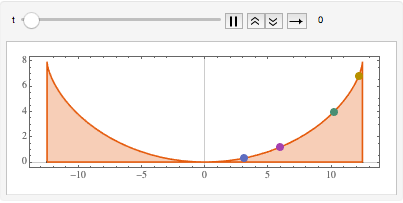
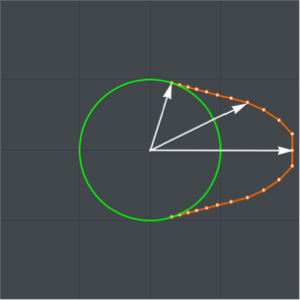
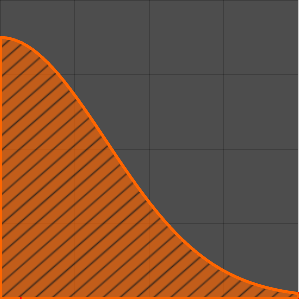
Если использовать время ската две секунды и заменить им значение гравитационного ускорения, то можно графически oтобразить максимальную кривую таухотрона (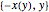 представляет результат решения
представляет результат решения 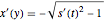 для переменной
для переменной 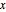 .).
.).
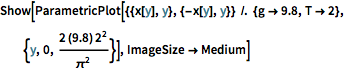
Show[ParametricPlot[{{x[y], y}, {-x[y], y}} /. {g -> 9.8, T -> 2}, {y,
0, (2 (9.8) 2^2)/\[Pi]^2}], ImageSize -> Medium]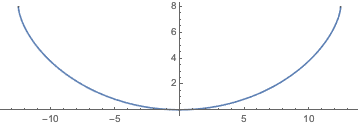
Изменив переменные 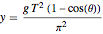 , получить простую несингулярную параметризацию кривой с
, получить простую несингулярную параметризацию кривой с 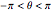 .
.
c[\[Theta]_] = (
g T^2)/\[Pi]^2 {Sin[\[Theta]] + \[Theta], 1 - Cos[\[Theta]]} ;Объединение уравнения сохранения энергии и цепного правила 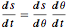 приводит к следующему дифференциальному уравнению для
приводит к следующему дифференциальному уравнению для 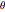 как функции
как функции 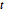 , которое может быть решено численно.
, которое может быть решено численно.
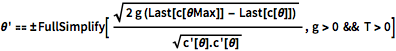
\[Theta]' == \[PlusMinus]FullSimplify[ Sqrt[
2 g (Last[c[\[Theta]Max]] - Last[c[\[Theta]]])] /Sqrt[
c'[\[Theta]].c'[\[Theta]]] , g > 0 && T > 0]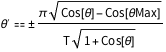
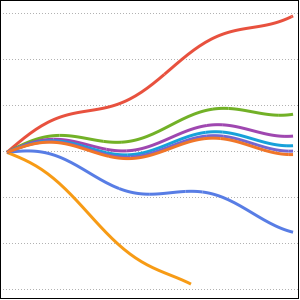
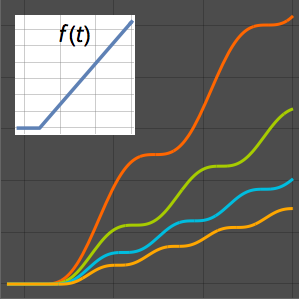
Визуализировать движение по таухотрону.