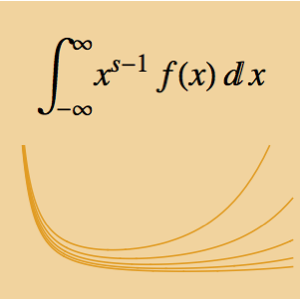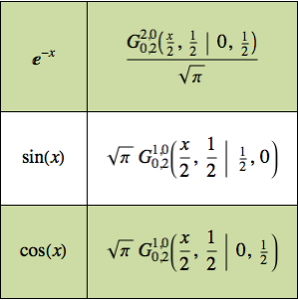Нахождение распределения заряда на сферической поверхности

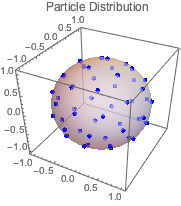
Найти положения, которые минимизируют электростатический потенциал для равнозаряженных частиц, свободно передвигающихся по сферической поверхности. Искомые положения называются равновесным распределением заряда.

Обозначить количество частиц буквой n.

In[1]:=

n = 50;

Допустим, что {x_i, y_i, z_i} являются декартовыми координатами частицы.

In[2]:=

vars = Join[Array[x, n], Array[y, n], Array[z, n]];

Для достижения равновесного распределения заряда необходимо минимизировать электростатический потенциал данной частицы.

In[3]:=

potential = Sum[((x[i] - x[j])^2 + (y[i] - y[j])^2 + (z[i] - z[j])^2)^-(1/ 2), {i, 1, n - 1}, {j, i + 1, n}];

Поскольку частицы находятся на сферической поверхности, их координаты должны удовлетворять общим амплитудным ограничениям.

In[4]:=

sphereconstr = Table[x[i]^2 + y[i]^2 + z[i]^2 == 1, {i, 1, n}];

Случайным образом, с помощью сферических координат, выбрать начальные точки на сферической поверхности.

In[5]:=

rpts = ConstantArray[1, n]; thetapts = RandomReal[{0, Pi}, n]; phipts = RandomReal[{-Pi, Pi}, n]; spherpts = Transpose[{rpts, thetapts, phipts}];

Перевести значения начальных точек в декартовы координаты.

In[6]:=

cartpts = CoordinateTransform["Spherical" -> "Cartesian", spherpts];

Перегруппировать начальные точки для соответствия порядку переменных.

In[7]:=

initpts = Flatten[Transpose[cartpts]];

Минимизировать электростатический потенциал по отношению к сферическому ограничению.

In[8]:=

sol = FindMinimum[{potential, sphereconstr}, Thread[{vars, initpts}]];

Извлечь из решения равновесные позиции частиц.

In[9]:=

solpts = Table[{x[i], y[i], z[i]}, {i, 1, n}] /. sol[[2]];

Отобразить полученный результат на графике.

In[10]:=

Show[ListPointPlot3D[solpts, PlotRange -> {{-1.1, 1.1}, {-1.1, 1.1}, {-1.1, 1.1}}, PlotStyle -> {{PointSize[.03], Blue}}, AspectRatio -> 1, BoxRatios -> 1, PlotLabel -> "Particle Distribution"], Graphics3D[{Opacity[.5], Sphere[]}]]

Out[10]=