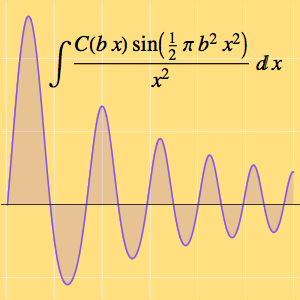Den Grenzwert einer Funktionsfolge untersuchen
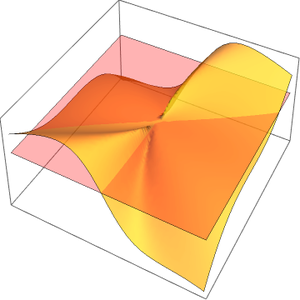
Dieses Beispiel veranschaulicht, wie sich die ungleichmäßige Konvergenz einer Funktionsfolge auf die Kommutativitäty der auf die Folge angewandten Beschränkungen auswirkt.
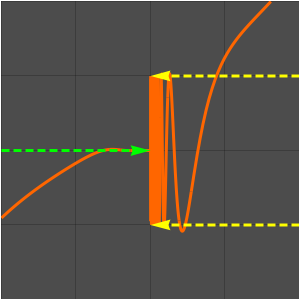
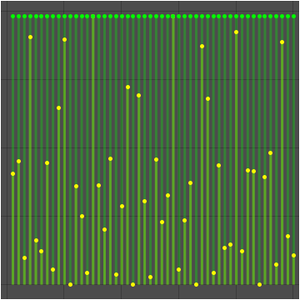
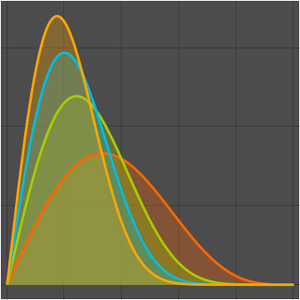
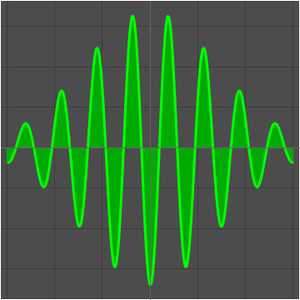
Die folgende Folge von Funktionen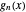 
konvergiert gegen Null in jedem Punkt 
.
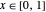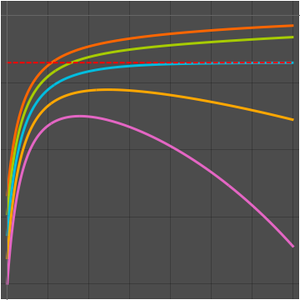
Der Maximalwert von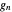 
an der Stelle 
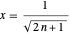divergiert wenn 
.
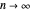Die zeigt, dass die Konvergenz der Folge nicht gleichmäßig ist.
Folglich gleicht der Grenzwert der Integrale nicht dem Integral des Grenzwerts.
