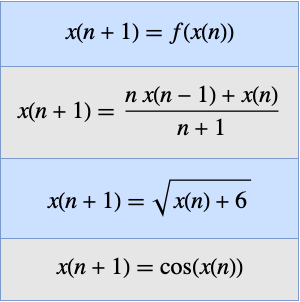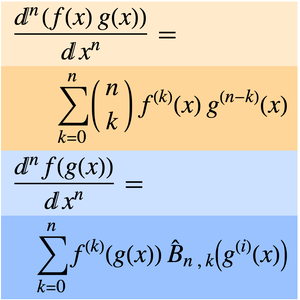Den Grenzwert einer Folge berechnen
Grenzwerte von Folgen treten häufig in der Mathematik auf und können auch dann existieren, wenn es keine entsprechenden Funktionsgrenzwerte gibt. Mit der Funktionalität DiscreteLimit der Version 12 können die Grenzwerte von Folgen, die in geschlossener Form oder durch formale Operatoren angegeben ist, berechnet werden. Die folgenden Beispiele illustrieren die Einsatzmöglichkeiten der neuen Funktion.
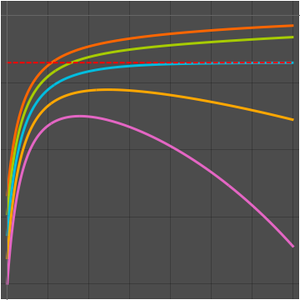
Ermitteln Sie den Grenzwert einer Folge.
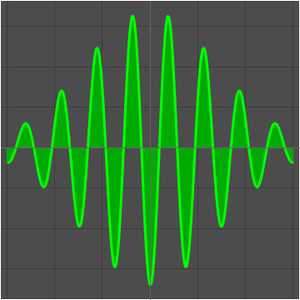
Visualisieren Sie die Folge.
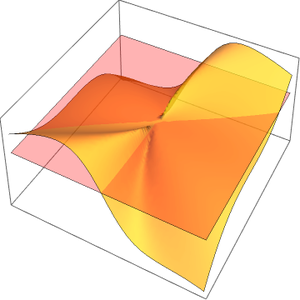
Ermitteln Sie den Grenzwert einer multivariaten Folge.
Visualisieren Sie die Folge.
Das folgende Beispiel verwendet die Stolz–Cesàro-Regel, eine diskrete Version der Regel von de l'Hôpital.
Ermitteln Sie den Grenzwert einer verschachtelten Inactive-Summe.
Ermitteln Sie den Grenzwert eines Inactive-Kettenbruchs.
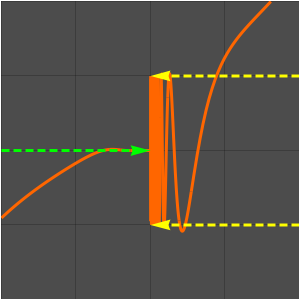
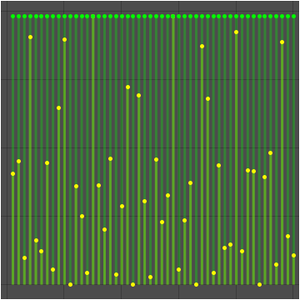
Das folgende Beispiel demonstriert, dass ein Funktionslimes zwar nicht existiert, der Grenzwert der entsprechenden Folge jedoch schon.
Definieren Sie eine trigonometrische Funktion.
Plotten Sie die Funktion und die Folge, die Sie durch Abtasten der Funktion bei den ganzen Zahlen erhalten haben.
Der Grenzwert der Funktion existiert nicht.
Der Grund dafür ist, dass die Funktionswerte zwischen -1 und 1 oszillieren.
Es gibt jedoch einen Grenzwert der Folge.
Der Grund dafür ist, dass die Folge bei allen abgetasteten Punkten konstant ist.