Output Regulation
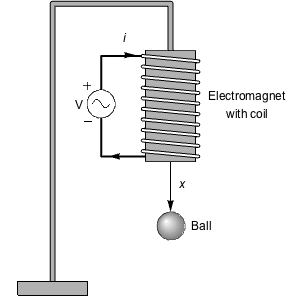
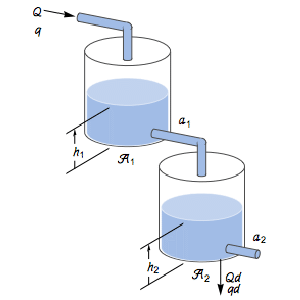
Regulate the height of the liquid in the lower tank whose net flow rate is subject to an exogenous disturbance. The control input is the flow into the upper tank.
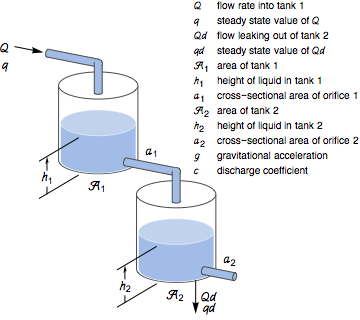 |
Use Bernoulli's law and mass balance to derive the resulting differential equations.
| In[1]:= | 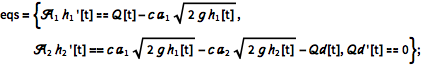 X |
Use steady-state operating values 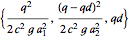 .
.
| In[2]:= | 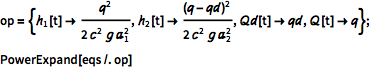 X |
| Out[2]= |
Define the corresponding nonlinear system with input 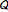 and output
and output 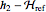 .
.
| In[3]:= | X |
| In[4]:= | X |
| Out[4]= | 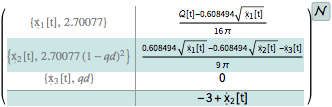 |
The feedback law.
| In[5]:= | X |
| Out[5]= | 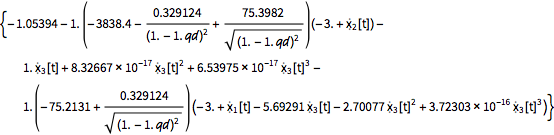 |
The closed-loop system.
| In[6]:= | X |
| Out[6]= |  |
A polynomial disturbance is approximated as a piecewise constant function.
| In[7]:= | X |
| In[8]:= | X |
| Out[8]= | 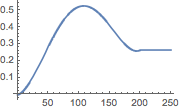 |
Assemble the simulation model and simulate the state responses.
| In[9]:= |  X |
| In[10]:= | X |
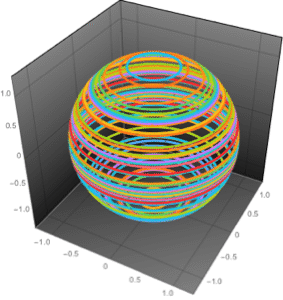
The plot shows that the desired regulation has been achieved.
| In[11]:= | X |
| Out[11]= | 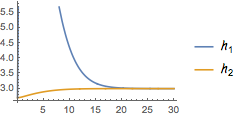 |