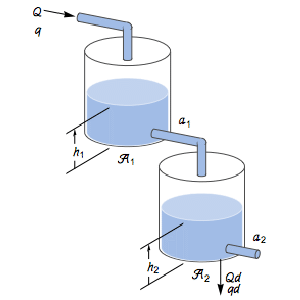
出力調節 

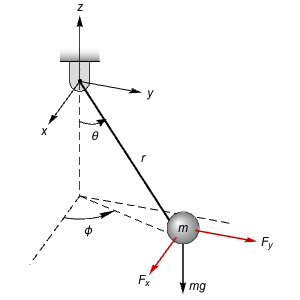
下のタンクの液体の高さを調節する．そのタンクの全体の流速は外因的な外乱に影響される．制御入力は上のタンクへの流れである．

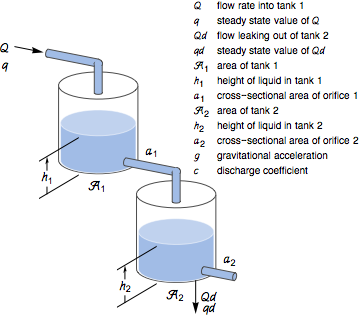ベルヌーイ(Bernoulli)の法則と質量平均を使って，結果の微分方程式を導き出す．

In[1]:=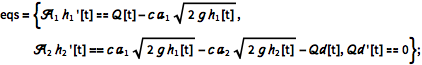

X eqs = {Subscript[\[ScriptCapitalA], 1] Subscript[\[ScriptH], 1]'[t] == \[ScriptCapitalQ][ t] - \[ScriptC] Subscript[\[ScriptA], 1] Sqrt[ 2 \[ScriptG] Subscript[\[ScriptH], 1][t]], Subscript[\[ScriptCapitalA], 2] Subscript[\[ScriptH], 2]'[t] == \[ScriptC] Subscript[\[ScriptA], 1] Sqrt[ 2 \[ScriptG] Subscript[\[ScriptH], 1][ t]] - \[ScriptC] Subscript[\[ScriptA], 2] Sqrt[ 2 \[ScriptG] Subscript[\[ScriptH], 2][ t]] - \[ScriptCapitalQ]\[ScriptD][ t], \[ScriptCapitalQ]\[ScriptD]'[t] == 0};

定常状態の動作値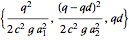を使う．

In[2]:=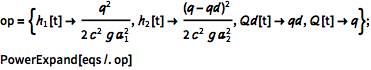

X op = {Subscript[\[ScriptH], 1][t] -> \[ScriptQ]^2/( 2 \[ScriptC]^2 \[ScriptG] \!\(\*SubsuperscriptBox[\(\[ScriptA]\), \(1\), \(2\)]\)), Subscript[\[ScriptH], 2][ t] -> (\[ScriptQ] - \[ScriptQ]\[ScriptD])^2/( 2 \[ScriptC]^2 \[ScriptG] \!\(\*SubsuperscriptBox[\(\[ScriptA]\), \(2\), \(2\)]\)), \ \[ScriptCapitalQ]\[ScriptD][ t] -> \[ScriptQ]\[ScriptD], \[ScriptCapitalQ][t] -> \[ScriptQ]}; PowerExpand[eqs /. op]

Out[2]=

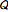入力 と出力 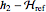を持つ対応する非線形系を定義する．

In[3]:=

X pars = {\[ScriptC] -> 0.7, \[ScriptG] -> 9.8, Subscript[\[ScriptCapitalA], 1] -> \[Pi] 4^2, Subscript[\[ScriptA], 1] -> \[Pi] 0.25^2, Subscript[\[ScriptCapitalA], 2] -> \[Pi] 3^2, Subscript[\[ScriptA], 2] -> \[Pi] 0.25^2, \[ScriptQ] -> 1, Subscript[\[ScriptCapitalH], ref] -> 3};

In[4]:=

X dtank = NonlinearStateSpaceModel[eqs, op[[1 ;; 3]], op[[-1]], {Subscript[\[ScriptH], 2][t] - Subscript[\[ScriptCapitalH], ref]}, t] /. pars

Out[4]=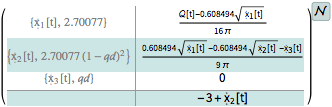

フィードバック法則．

In[5]:=

X \[ScriptK] = FullInformationOutputRegulator[dtank, {-0.5, -1}] // Simplify

Out[5]=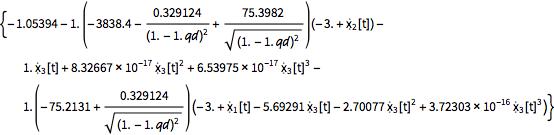

閉ループ系．

In[6]:=

X csys = SystemsModelStateFeedbackConnect[dtank, \[ScriptK]] // Simplify

Out[6]=

多項式外乱は区分的な定数関数として近似される．

In[7]:=

X \[ScriptD] = -0.003 + 0.0013 x + 0.00016 x^2 - 1.613 10^-6 x^3 + 4.069 10^-9 x^4; Subscript[\[ScriptD], \[ScriptA]] = Piecewise[Table[{\[ScriptD], x <= t < x + 1}, {x, 0, 200, 1}], 0.2634];

In[8]:=

X Plot[Subscript[\[ScriptD], \[ScriptA]], {t, 0, 250}, Exclusions -> None]

Out[8]=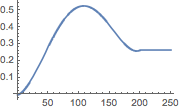

シミュレーションモデルを組み立て，状態応答をシミュレーションする．

In[9]:=

X csys1 = NonlinearStateSpaceModel[csys, Join[op[[1 ;; 2]], {{\[ScriptCapitalQ]\[ScriptD][t], 0}}] /. pars /. \[ScriptQ]\[ScriptD] -> 0] /. \[ScriptQ]\[ScriptD] -> Subscript[\[ScriptD], \[ScriptA]];

In[10]:=

X sr = StateResponse[csys1, 0, {t, 0, 50}];

プロットは，希望の調節が達成できたことを示す．

In[11]:=

X Plot[Evaluate@sr[[{1, 2}]], {t, 0, 30}, PlotLegends -> {"\!\(\*SubscriptBox[\(\[ScriptH]\), \(1\)]\)", "\!\(\*SubscriptBox[\(\[ScriptH]\), \(2\)]\)"}]

Out[11]=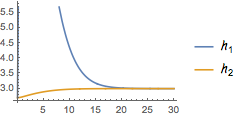