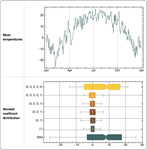
Mathematica 8 引入了一套完全集成的小波分析系统，包括收集了大量小波族，以及离散小波变换和连续小波变换的多种变体。小波变换易于使用，每个变换产生一个符号式变换表示，使之易于调用、操作和由可视化变换系数组成的树。Mathematica 新的小波功能使用户可以直接使用多维数据、声音以及图像，而无需任何转换。

• 收集了大量离散和连续小波族。 »
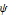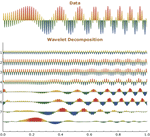
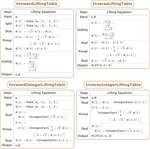
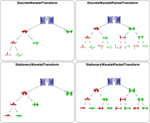
• 所有小波族的任意精度的尺度函数（）、小波函数（）和滤波系数。 »
• 离散小波变换（DWT）、平稳小波变换（SWT）和提升小波变换（LWT），及其逆变换。 »
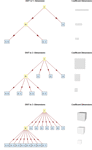
• 离散小波包变换（DWPT）和平稳小波包变换（SWPT），包括最佳基计算。 »
• 计算任意维数数据的离散小波变换。 »
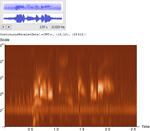
• 离散变换可以直接操作于声音和图像。 »
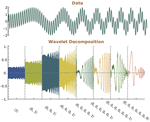
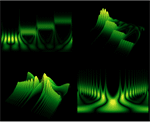
• 连续小波变换（CWT），包括逆变换（ICWT）。 »
• 直接计算声音的连续小波变换。 »
• 对所有变换均有高度的优化性能和任意精度支持。
• 所有变换均产生符号式小波分解，使之可以被进一步操纵。 »
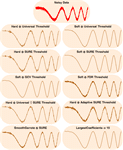
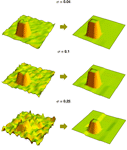
• 对小波阈值方法的扩展支持。 »
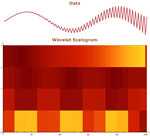
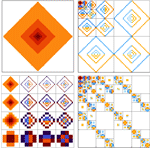
• 小波可视化函数，包括尺度谱图和金字塔图。 »

连续小波族 »	离散小波族 »	获取小波族的属性 »
离散小波变换（DWT） »	平稳小波变换（SWT） »	提升小波变换（LWT） »
离散小波包变换（DWPT） »	平稳小波包变换（SWPT） »	比较离散小波变换 »
变换任意维数的数据 »	计算高精度的小波变换 »	连续小波变换（CWT） »
直接变换多维数组 »	直接变换声音 »	直接变换图像 »
使用共同 x 轴图可视化小波变换 »	使用共同 y 轴图可视化小波变换 »	使用尺度谱图可视化离散小波变换 »
小波矩阵图 »	小波图像图 »	可视化三维的尺度谱图 »
使用不同的小波阈值方法 »	对多维数据加阈值 »	图像降噪 »
计算小波最佳基 »	二维离散小波包变换 »	动态产生提升方程组 »
小波图像的融合 »	图像处理 »	可视化小波系数分布 »

相关函数

WaveletPhi  WaveletPsi  WaveletFilterCoefficients  BattleLemarieWavelet  BiorthogonalSplineWavelet  CDFWavelet  CoifletWavelet  DaubechiesWavelet  DGaussianWavelet  GaborWavelet  HaarWavelet  MexicanHatWavelet  MeyerWavelet  MorletWavelet  PaulWavelet  ReverseBiorthogonalSplineWavelet  ShannonWavelet  SymletWavelet  ContinuousWaveletTransform  DiscreteWaveletTransform  InverseContinuousWaveletTransform  InverseWaveletTransform  LiftingWaveletTransform  StationaryWaveletTransform  WaveletMapIndexed  WaveletThreshold  WaveletBestBasis  WaveletScalogram  WaveletListPlot  WaveletMatrixPlot  WaveletImagePlot  ArrayPad  ContinuousWaveletData  DiscreteWaveletData