固定された膜の固有関数を計算する

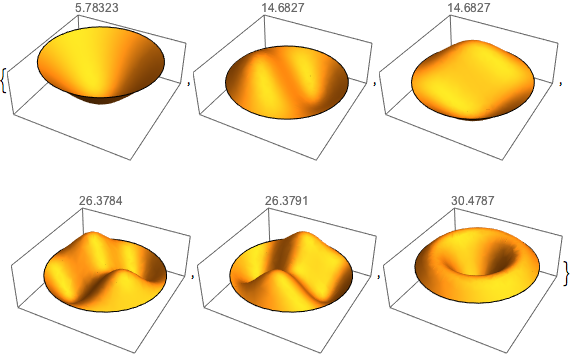
辺が固定された円形膜の固有関数を小さい方から6個計算する．

ラプラス演算子を指定する．

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}];

ディリクレ境界条件を指定する．

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

固有値と固有関数を小さい方から6個求める．

In[3]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y], {x, y} \[Element] Disk[], 6];

固有値を調べる．

In[4]:=

vals

Out[4]=

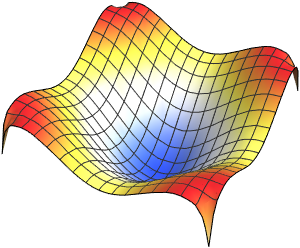
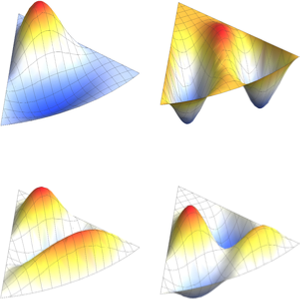
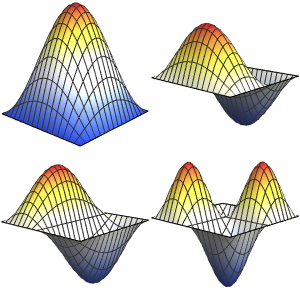
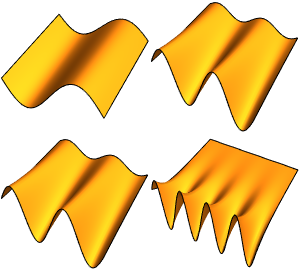
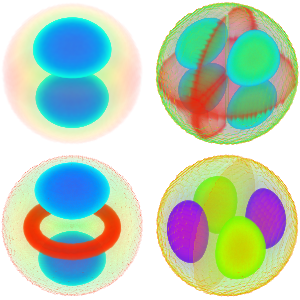
固有関数を可視化する．

In[5]:=

Table[Plot3D[funs[[i]], {x, y} \[Element] Disk[], PlotRange -> All, PlotLabel -> vals[[i]], PlotTheme -> "Minimal"], {i, Length[vals]}]

Out[5]=