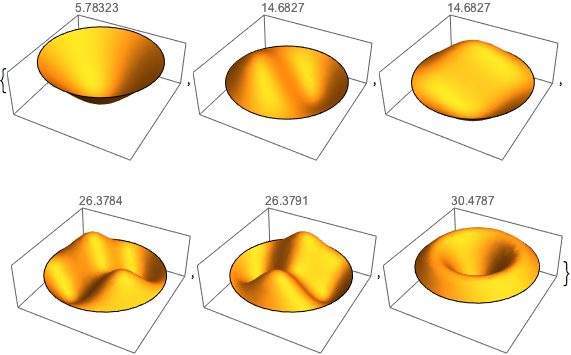
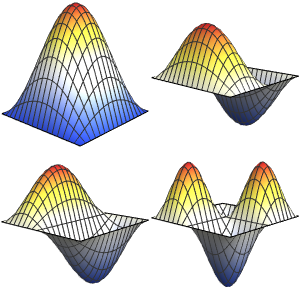
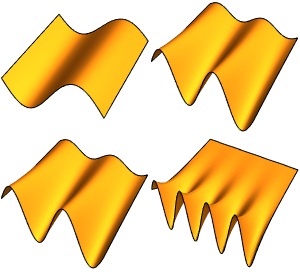
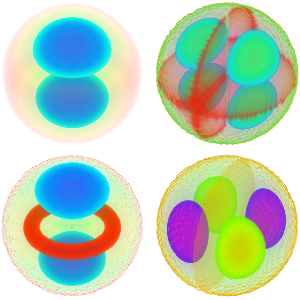
计算周边固定的薄膜的特征函数

计算边缘被固定住的圆形薄膜的前六个本征函数.

设定一个拉普拉斯算子.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}];

设定狄利克雷边界条件.

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

找出最小的六个特征值和特征函数.

In[3]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y], {x, y} \[Element] Disk[], 6];

查看特征值.

In[4]:=

vals

Out[4]=

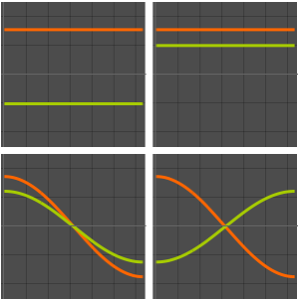
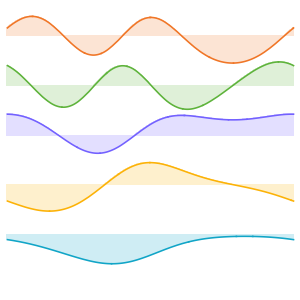
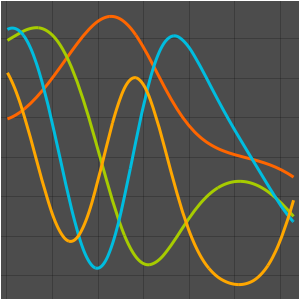
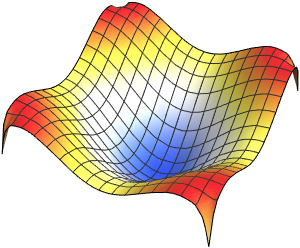
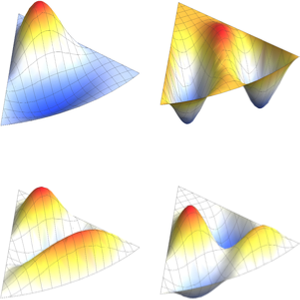
可视化特征函数.

In[5]:=

Table[Plot3D[funs[[i]], {x, y} \[Element] Disk[], PlotRange -> All, PlotLabel -> vals[[i]], PlotTheme -> "Minimal"], {i, Length[vals]}]

Out[5]=