Wolfram Language™

Calculez les fonctions propres pour une membrane serrée

Calculez les six premières fonctions propres d'une membrane circulaire dont les arêtes sont serrées.

Spécifiez un opérateur Laplacien.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}];

Spécifiez une condition aux limites de Dirichlet.

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

Trouvez les six plus petites valeurs et fonctions propres.

In[3]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y], {x, y} \[Element] Disk[], 6];

Inspectez les valeurs propres.

In[4]:=

vals

Out[4]=

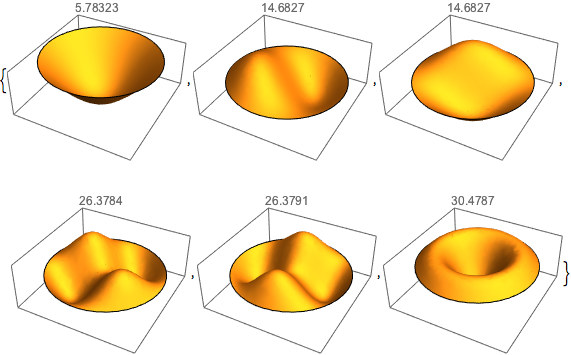
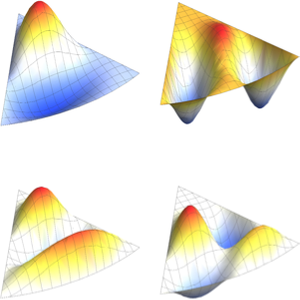
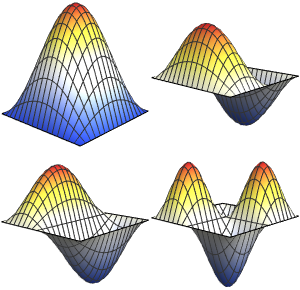
Visualisez les fonctions propres.

In[5]:=

Table[Plot3D[funs[[i]], {x, y} \[Element] Disk[], PlotRange -> All, PlotLabel -> vals[[i]], PlotTheme -> "Minimal"], {i, Length[vals]}]

Out[5]=