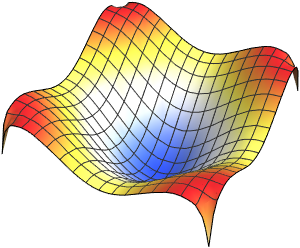
Investigue uma equação de Laplace Equation em um toro: Novos Recursos do Wolfram Language 11

Investigue uma equação de Laplace Equation em um toro

Encontre os cinco menores valores e funções próprios de uma equação de Laplace em um toro quadrado com uma restrição de Dirichlet.

Especifique as condições de contorno periódicas em um quadrado de comprimento 1.

In[1]:=

torusBCs = {u[0, y] == u[1, y], u[x, 0] == u[x, 1]};

Especifique um valor na origem. Pelas condições periódicas, este também deve ser o valor das outras três arestas do quadrado.

In[2]:=

constraint = DirichletCondition[u[x, y] == 0, x == 0 && y == 0];

Calcule os valores e as funções próprios.

In[3]:=

{vals, funs} = 
  NDEigensystem[
   Join[{-Laplacian[u[x, y], {x, y}], constraint}, torusBCs], 
   u[x, y], {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 4];

Inspecione os valores próprios.

In[4]:=

vals

Out[4]=

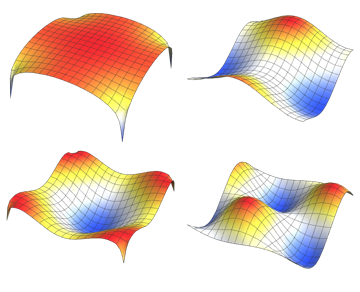
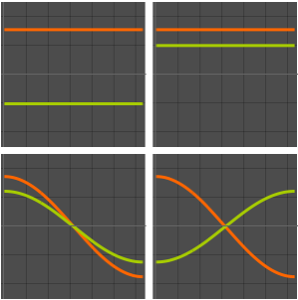
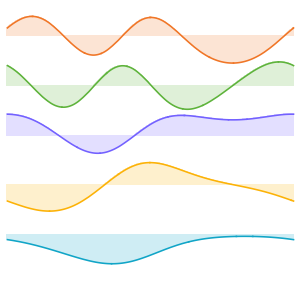
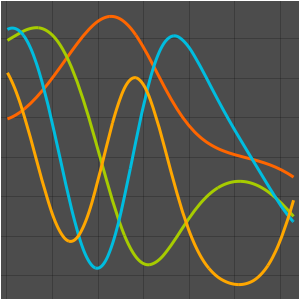
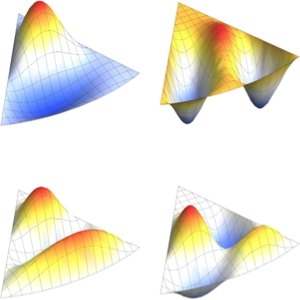
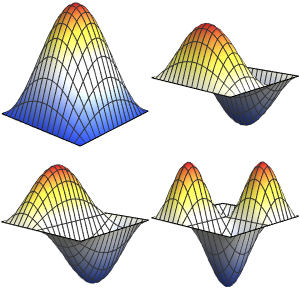
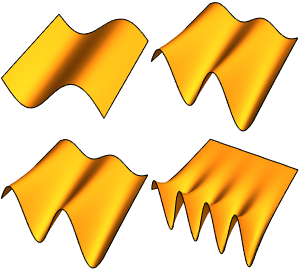
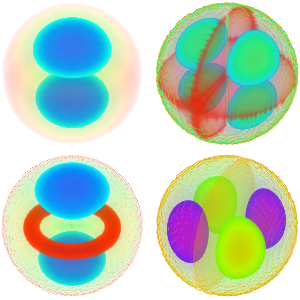
Visualize as funções próprias.

mostre o input completo da Wolfram Language

In[5]:=

ImageCollage[
 Plot3D[#, {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 
    ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None, 
    PlotRange -> All, PlotStyle -> {Specularity[White, 20]}] & /@ 
  funs, Background -> Transparent]

Out[5]=