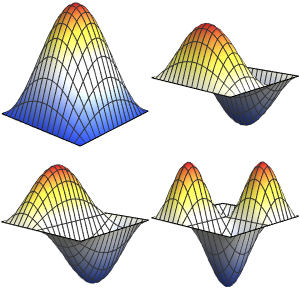
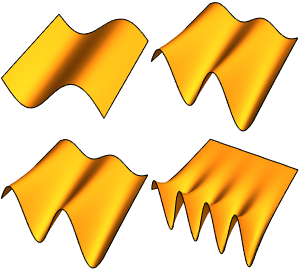
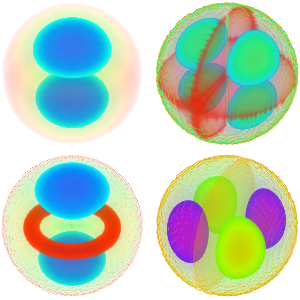
Gere uma expansão de função própria
Calcule a expansão da função própria da função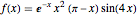 
em relação a base proporcionada pelo operador laplaciano com condição de limite de contorno de Dirichlet no intervalo 
.
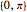In[1]:=
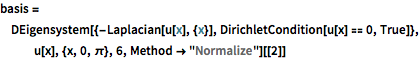
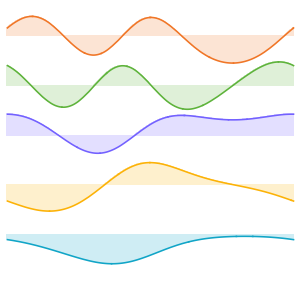
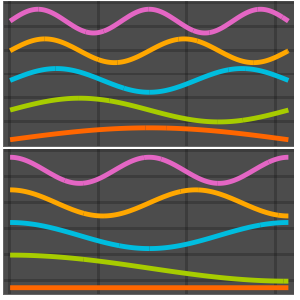
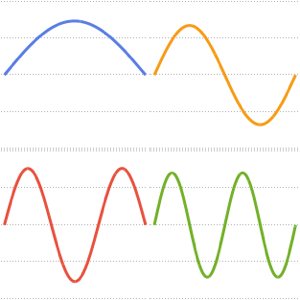
basis = DEigensystem[{-Laplacian[u[x], {x}],
DirichletCondition[u[x] == 0, True]}, u[x], {x, 0, \[Pi]}, 6,
Method -> "Normalize"][[2]]Out[1]=
Calcule os coeficientes de Fourier para a função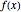 
.
In[2]:=
f[x_] := E^(-x) x^2 (\[Pi] - x) Sin[4 x]In[3]:=
coeffs = (Table[Integrate[f[x] basis[[i]], {x, 0, Pi}], {i, 6}] //
FullSimplify);Defina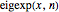 
como a 
soma parcial da expansão.
In[4]:=
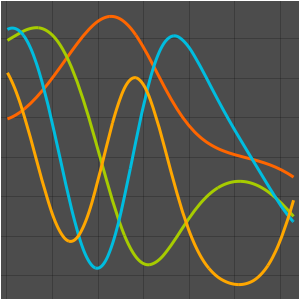
eigexp[x_, n_] := Sum[coeffs[[i]] basis[[i]], {i, n}]In[5]:=
eigexp[x, 3] // NOut[5]=
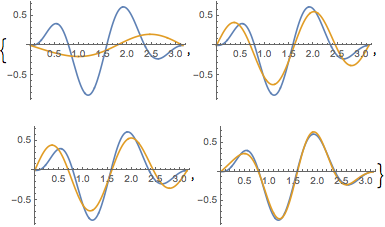
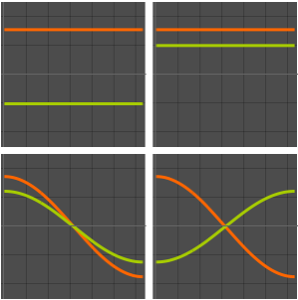
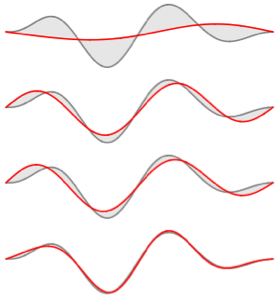
Compare a função com sua expansão da função própria para diferentes valores de 
.
In[6]:=
Table[Plot[{f[x], eigexp[x, i]} // Evaluate, {x, 0, Pi}], {i, 3, 6}]Out[6]=
