Encontre o valor próprio de Aharonov–Bohm : Novos Recursos do Wolfram Language 11

Encontre o valor próprio de Aharonov–Bohm

O efeito de Aharonov–Bohm é um fenômeno da mecânica quântica, onde uma partícula carregada detecta um potencial eletromagnético mesmo que o campo magnético dentro da região onde a partícula pode mover é zero. Neste exemplo, a equação de Schrödinger para um campo magnético fixo concentrado em uma linha perpendicular ao domínio da partícula é considerada.

Especifique a região como um setor no plano 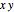centrado sobre o eixo .

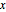In[1]:=

\[CapitalOmega] = Disk[{0, 0}, 1, {-\[Pi]/8, \[Pi]/8}];

Especifique o operador de Aharonov–Bohm. O campo magnético é restrito ao eixo .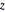

In[2]:=

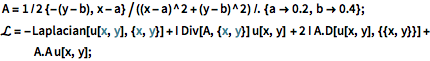
 A = 1/2 {-(y - b), x - a}/((x - a)^2 + (y - b)^2) /. {a -> 0.2, 
    b -> 0.4};
\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}] + 
   I Div[A, {x, y}] u[x, y] + 2 I A.D[u[x, y], {{x, y}}] + 
   A.A u[x, y];

Especifique as condições de contorno de Dirichlet em todo o contorno.

In[3]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

Calcule seis valores e funções próprios do operador.

In[4]:=

{vals, funs} = 
  NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, 
   u[x, y], {x, y} \[Element] \[CapitalOmega], 6];

Especifique os valores próprios.

In[5]:=

vals

Out[5]=

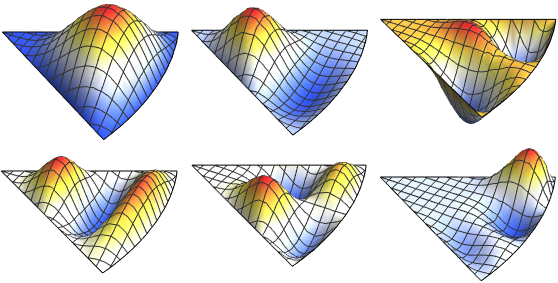
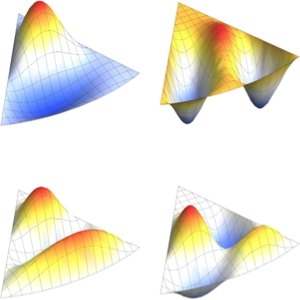
Visualize a parte real das funções próprias.

mostre o input completo da Wolfram Language

In[6]:=

Grid[Partition[
   Plot3D[Re[#], {x, y} \[Element] \[CapitalOmega], 
      ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None,
       PlotRange -> All, PlotStyle -> {Specularity[White, 20]}, 
      Method -> {"ShrinkWrap" -> True}] & /@ funs, 3], 
  Background -> Transparent] // Quiet

Out[6]=