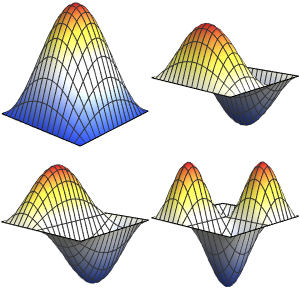
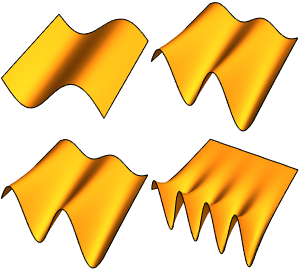
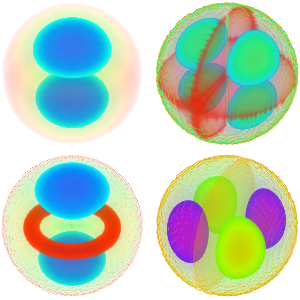
Encontre as funções simbólicas próprias de um laplaciano em 1D

Especifique um operador laplaciano em 1D.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}];

Especifique as condições de contorno de Dirichlet homogêneos para as funções próprias.

In[2]:=

\[ScriptCapitalB]1 = DirichletCondition[u[x] == 0, True];

Encontre os cinco menores valores e funções próprios.

In[3]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]1}, u[x], {x, 0, \[Pi]}, 5];

Inspecione os valores próprios.

In[4]:=

vals

Out[4]=

Inspecione as funções próprias.

In[5]:=

funs

Out[5]=

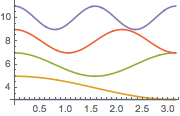
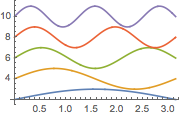
Visualize as funções próprias.

In[6]:=

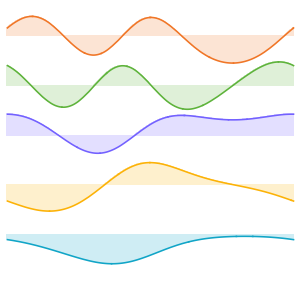
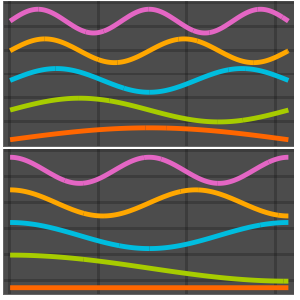
Plot[Evaluate[funs + 2 Range[5]], {x, 0, \[Pi]}]

Out[6]=

Especifique uma condição de contorno de Neumann homogêneo.

In[7]:=

\[ScriptCapitalB]2 = NeumannValue[0, True];

Encontre os cinco menores valores e funções próprios.

In[8]:=

{vals, funs} = DEigensystem[\[ScriptCapitalL] + \[ScriptCapitalB]2, u[x], {x, 0, \[Pi]}, 5];

Inspecione os valores próprios. Em relação às condições de Dirichlet, um modo zero foi adicionado.

In[9]:=

vals

Out[9]=

Senos têm substituído cossenos nas funções próprias.

In[10]:=

funs

Out[10]=

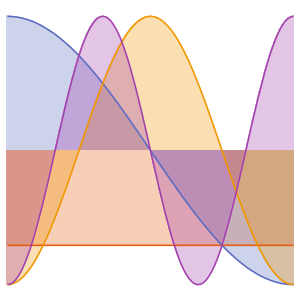
Visualize as funções próprias.

In[11]:=

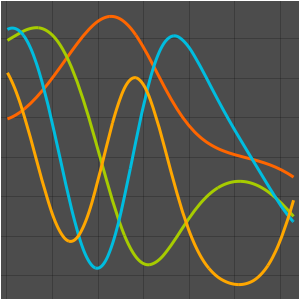
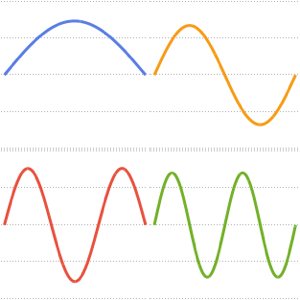
Plot[Evaluate[funs + 2 Range[5]], {x, 0, \[Pi]}]

Out[11]=