Wolfram Language™

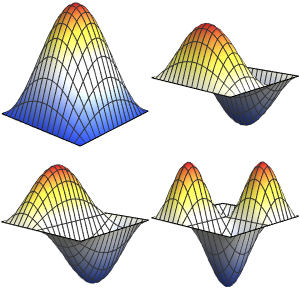
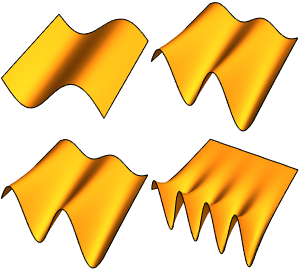
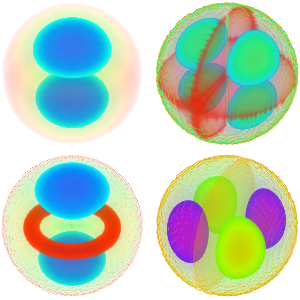
Investigue o problema próprio de um operador de onda

Encontre os quatro menores valores próprios e funções próprias de uma equação de onda generalizada 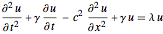sobre uma região em 1D.

Estabeleça um operador de onda generalizado .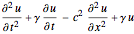

In[1]:=

\[Gamma] = 1.3; c = 1.1; op = D[u[t, x], {t, 2}] + \[Gamma] D[u[t, x], {t, 1}] - c^2 D[u[t, x], {x, 2}] + \[Gamma] u[t, x];

Encontre os quatro menores valores próprios e funções próprias sobre uma região em 1D.

In[2]:=

{vals, funs} = NDEigensystem[op == 0, u[t, x], t, {x, 0, \[Pi]}, 4];

Inspecione os valores próprios.

In[3]:=

vals

Out[3]=

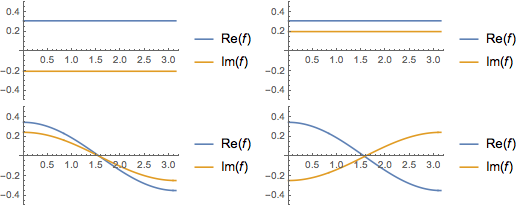
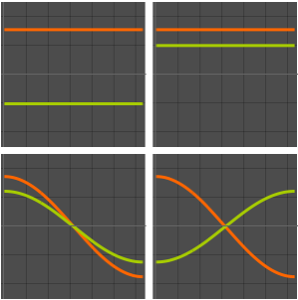
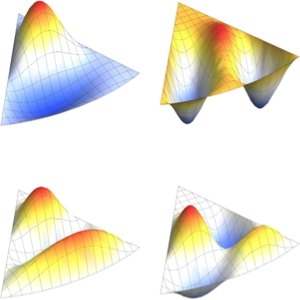
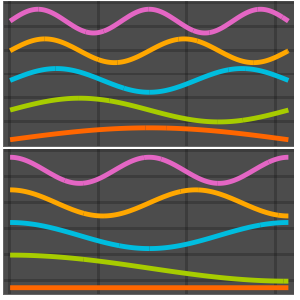
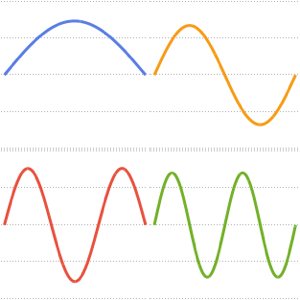
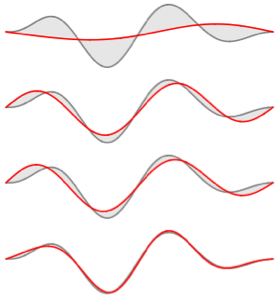
Visualize as partes reais e imaginárias das funções próprias. Observe que as funções próprias vêm em pares conjugados como os valores próprios.

In[4]:=

Grid[Partition[ Plot[Evaluate[ReIm[#]], {x, 0, \[Pi]}, PlotRange -> .5, PlotLegends -> {HoldForm@Re[f], HoldForm@Im[f]}] & /@ funs, 2]]

Out[4]=