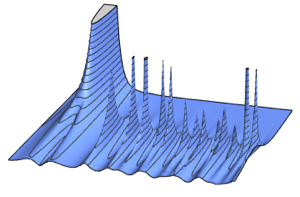
Интервалы между собственными значениями в гауссовых распределениях : Новое в системе Wolfram Language 11

Интервалы между собственными значениями в гауссовых распределениях

Интервалы между собственными значениями (разница между последовательными собственными значениями) матричных распределений имеют универсальную ограничивающую форму, которую можно найти во многих системах в природе, таких как расстояние между энергетическими уровнями атомов тяжёлых металлов.

Отберите интервалы между собственными значениями 2×2 матриц различных гауссовых ансамблей.

In[1]:=

gaussiandists = {GaussianOrthogonalMatrixDistribution[2], 
   GaussianUnitaryMatrixDistribution[2], 
   GaussianSymplecticMatrixDistribution[2]};

In[2]:=

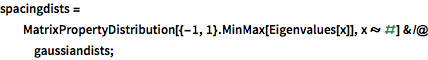
spacingdists = 
  MatrixPropertyDistribution[{-1, 1}.MinMax[Eigenvalues[x]], 
     x \[Distributed] #] & /@ gaussiandists;

In[3]:=

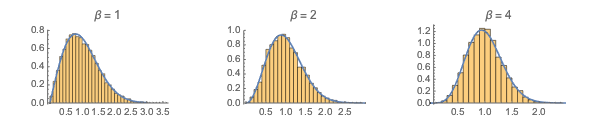
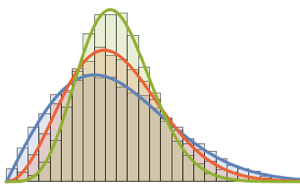
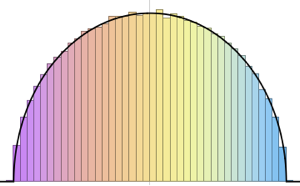
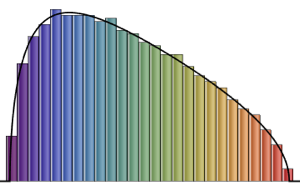
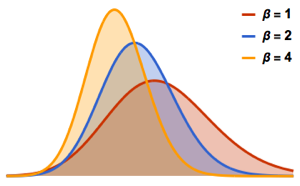
gaps = Normalize[RandomVariate[#, 10000], Mean] & /@ spacingdists;

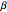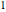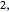Сравните гистограммы для каждого распределения с его замкнутой формой, также известной как предположение Вигнера для индексов Дайсона от , и .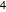

In[4]:=

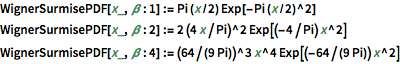
WignerSurmisePDF[x_, \[Beta] : 1] := Pi (x/2) Exp[-Pi (x/2)^2]
WignerSurmisePDF[x_, \[Beta] : 2] := 2 (4 x/Pi)^2 Exp[(-4/Pi) x^2]
WignerSurmisePDF[
  x_, \[Beta] : 4] := (64/(9 Pi))^3 x^4 Exp[(-64/(9 Pi)) x^2]

код на языке Wolfram Language целиком

In[5]:=

histogram = Histogram[#, {0.1}, PDF] & /@ gaps;
plot = Plot[WignerSurmisePDF[x, #] , {x, 0, 3}] & /@ {1, 2, 4};
GraphicsRow@
 MapThread[
  Show[#1, #2, ImageSize -> 180, 
    PlotLabel -> Row[{"\[Beta] = ", #3}]] &, {histogram, 
   plot, {1, 2, 4}}]

Out[5]=