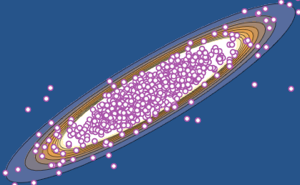
Гауссовы ансамбли (ГОА, ГУА, ...): Новое в системе Wolfram Language 11

Гауссовы ансамбли (ГОА, ГУА, ...)

Гауссовы ансамбли - это семейства нормально распределённых случайных матриц с неизменными распределениями при различных унитарных трансформациях. Они являются хорошо изученными, частично благодаря аналитической разрешимости, но также потому, что присоединённые спектры точно приближены к тем, которые принадлежат многим системам с большой степенью свободы. Примеры данных систем присутствуют в физике, финансах, и биологии.

Матрицы из гауссова ортогонального ансамбля (ГОА) симметричны. »

In[1]:=

goe = RandomVariate[GaussianOrthogonalMatrixDistribution[5]];

In[2]:=

SymmetricMatrixQ[goe]

Out[2]=

Матрицы из гауссова унитарного ансамбля (ГУА) эрмитовы. »

In[3]:=

gue = RandomVariate[GaussianUnitaryMatrixDistribution[5]];

In[4]:=

HermitianMatrixQ[gue]

Out[4]=

Матрицы из гауссова симплектического ансамбля (ГСА) симплектически эрмитовы. »

код на языке Wolfram Language целиком

In[5]:=

symplecticMatrixQ[m_] := 
  With[{\[ScriptCapitalJ] = 
     KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]]},
   Conjugate[m].\[ScriptCapitalJ] == \[ScriptCapitalJ].m
   ];

In[6]:=

gse = RandomVariate[GaussianSymplecticMatrixDistribution[5]];

In[7]:=

symplecticMatrixQ[gse] && HermitianMatrixQ[gse]

Out[7]=

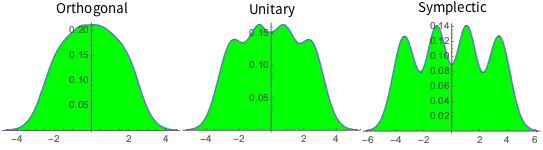
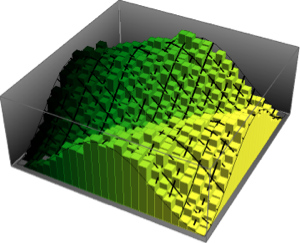
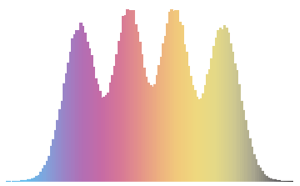
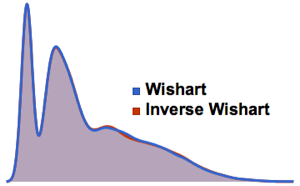
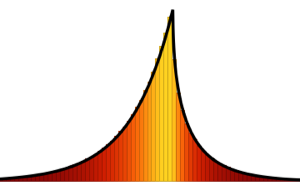
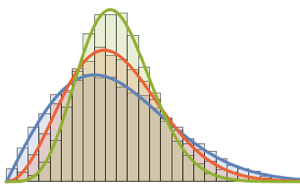
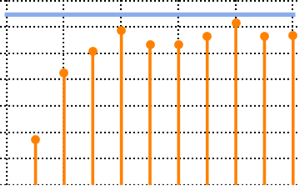
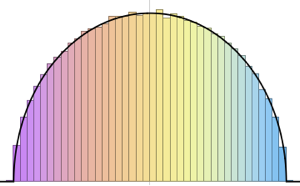
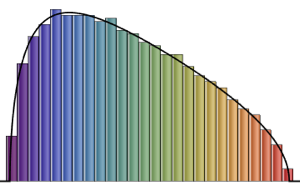
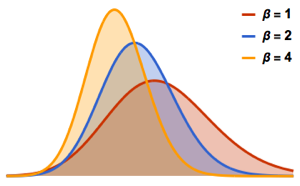
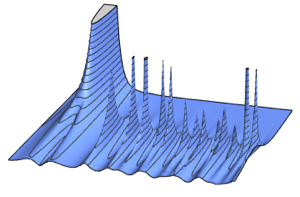
Распределение собственных значений для матриц из гауссовых ансамблей в маленьких измерениях.

код на языке Wolfram Language целиком

In[8]:=

eigs = Flatten[
     RandomVariate[
      MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #], 
      10^5]] & /@ {GaussianOrthogonalMatrixDistribution[4], 
    GaussianUnitaryMatrixDistribution[4], 
    GaussianSymplecticMatrixDistribution[4]};
Row[MapThread[
  SmoothHistogram[#1, "Scott", Frame -> None, 
    PlotLegends -> Placed[#2, Above], Filling -> Axis, 
    FillingStyle -> Green] &,
  {eigs, {Style["Orthogonal", 15], Style["Unitary", 15], 
    Style["Symplectic", 15]}}]]

Out[8]=