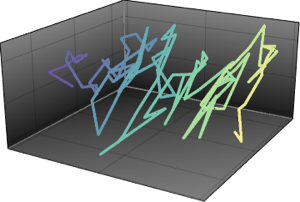
Броуновское движение для КУА

Броуновское движение может быть создано при помощи инфинитезимальной образующей. Броуновское движение на множестве унитарных матриц может быть создано инфинитезимальными образующими из гауссова унитарного ансамбля. Стационарное распределение этого броуновского движения тогда становится идентичным распределению КУА.

In[1]:=

mats = RandomVariate[GaussianUnitaryMatrixDistribution[0.1, 2], 100000]; mats = Table[MatrixExp[I mat], {mat, mats}];

Сгенерируйте броуновскую траекторию с начальными точками, выбранными в КУА.

In[2]:=

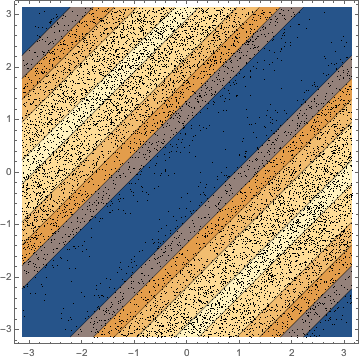
initial = RandomVariate[CircularUnitaryMatrixDistribution[2]]; res = FoldList[#2.#1 &, initial, mats];

Рассчитайте фазы собственных значений и сравните их с плотностью вероятности собственных значений матриц из КУА.

In[3]:=

phases = RandomSample /@ Arg[Eigenvalues /@ res];

In[4]:=

Show[ ContourPlot[ 1/(8 Pi^2) Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, Pi}, {\[Phi]2, -Pi, Pi}], ListPlot[Take[phases, {1, -1, 10}], ImageSize -> Medium, PlotStyle -> Black, PlotTheme -> "Detailed"], ImageSize -> Medium]

Out[4]=