Распределение Марченко-Пастура

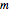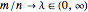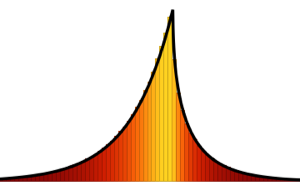
Распределение Марченко-Пастура является допредельным распределением собственных значений матриц Уишарта, где матричное измерение и степени свободы стремятся к бесконечности в отношении . Для 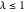распределение не имеет точечной массы, а функция плотности вероятности чётко определена.

In[1]:=

PDF[MarchenkoPasturDistribution[1/2], x]

Out[1]=

In[2]:=

Plot[PDF[MarchenkoPasturDistribution[1/2], x], {x, 0, 3}, PlotRange -> All, Exclusions -> None, Filling -> Axis, PlotTheme -> "Detailed", ImageSize -> Medium, PlotLegends -> None]

Out[2]=

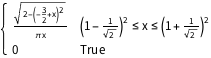
Попробуйте распределение Уишарта с идентичной нормированной матрицей и рассчитайте нормированные собственные значения.

In[3]:=

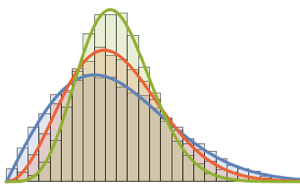
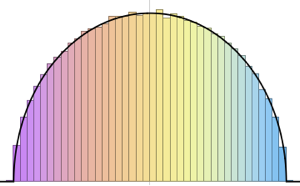
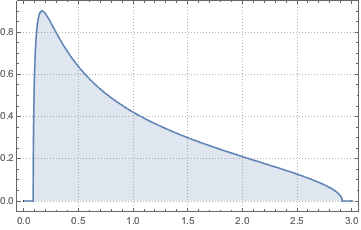
n = 10^4; m = 10^3; eigs = RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x]/n, x \[Distributed] WishartMatrixDistribution[n, IdentityMatrix[m]]]];

Сравните полученный результат с функцией плотности Марченко-Пастура.

In[4]:=

Show[Histogram[eigs, {0.05}, "PDF", ImageSize -> Medium, PlotTheme -> "Detailed"], Plot[PDF[MarchenkoPasturDistribution[m/n], x], {x, 0, 1.8}, PlotTheme -> "Detailed", PlotLegends -> None, Exclusions -> None]]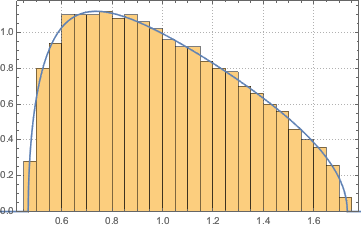

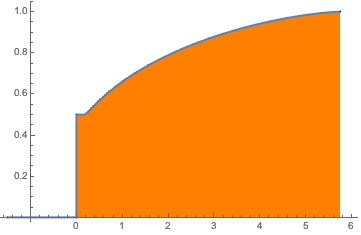
Out[4]=

Для 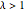матрица Уишарта является особенной. С вероятностью 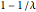распределение имеет точечную массу при .

In[5]:=

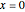m = 500; n = 2 m; CDF[MarchenkoPasturDistribution[n/m], 0]

Out[5]=

Сгенерируйте особенную матрицу Уишарта с тождественным ковариантом и рассчитайте нормированные собственные значения.

In[6]:=

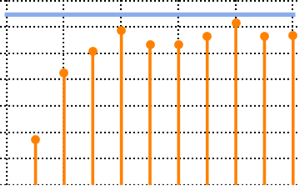
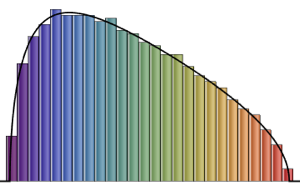
matrix = Transpose[#].# &[RandomVariate[NormalDistribution[], {m, n}]]; eigvs = Chop[Eigenvalues[matrix]/m];

Существует пробел в плотности собственных значений в области 0, и столбик 0 гистограммы имеет большую плотность.

In[7]:=

Histogram[eigvs, {0.05}, PDF, PlotRange -> 1, ChartStyle -> Orange, ImageSize -> Medium]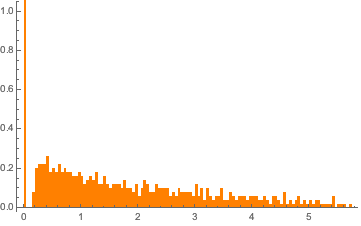

Out[7]=

Приблизьте MarchenkoPasturDistribution к собственным значениям.

In[8]:=

edist = EstimatedDistribution[eigvs, MarchenkoPasturDistribution[\[Lambda], 1]]

Out[8]=

Функция подобранного распределения демонстрирует простой разрыв в начале координат.

In[9]:=

Show[Histogram[eigvs, {0.05}, CDF, ChartStyle -> Orange], Quiet@Plot[CDF[edist, x], {x, -1.5, 5.75}, Exclusions -> None, PlotStyle -> Thick], ImageSize -> Medium, AxesOrigin -> {-1, 0}, PlotRange -> {{-1.5, 6}, {0, 1}}]

Out[9]=