Язык Wolfram Language™

Беспорядочное вращение

CircularRealMatrixDistribution представляет равномерное распределение ортогональных квадратных матриц с размером массива , также известное как мера Хаара на ортогональной группе 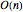. Матрицы, сгенерированные согласно данному распределению, могут выступать в роли операторов вращения для векторов в -мерном векторном пространстве.

Определите распределение случайных векторов, полученных путём вращения фиксированного трёхмерного вектора (0,0,1) случайной матрицей из CircularRealMatrixDistribution размера массива 3.

In[1]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[r.{0, 0, 1}, r \[Distributed] CircularRealMatrixDistribution[3]];

Используйте данное распределение для отбора точек на поверхности единичной сферы.

In[2]:=

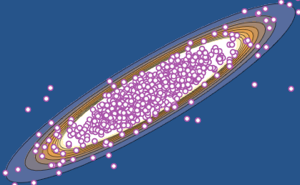
points = RandomVariate[\[ScriptCapitalD], 10^3];

Проверьте, принадлежат ли все отобранные точки единичной сфере.

In[3]:=

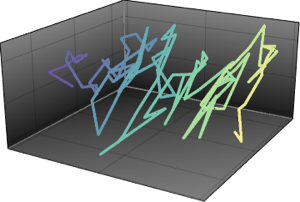
AllTrue[points, RegionMember[Sphere[3]]]

Out[3]=

Графически изобразите отобранные точки с исходным вектором.

In[4]:=

Graphics3D[{{Gray, PointSize[Small], Point[points]}, {Red, Thick, Arrow[{{0, 0, 0}, {0, 0, 1}}]}}, Axes -> True]

Out[4]=

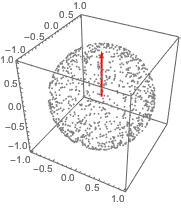
Параметр площади поверхности сферы задан в цилиндрических координатах через .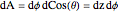

In[5]:=

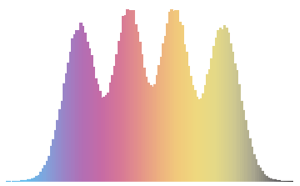
{x, y, z} = Transpose[points]; \[Phi] = ArcTan[y/x];

Проверьте, являются ли маргинальные распределения и 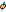равномерными.

In[6]:=

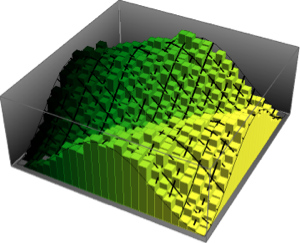
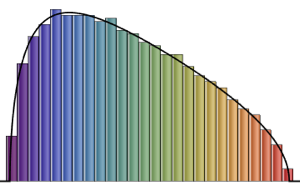
Histogram[#, 20, PDF] & /@ {\[Phi], z}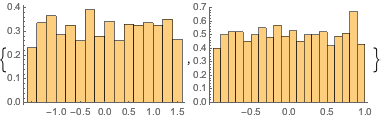

Out[6]=

Убедитесь, равномерно ли распределены отобранные точки на поверхности сферы, проверив равномерность совместного распределения 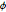и .

In[7]:=

Graphics[Point[Transpose[{\[Phi], z}]], Axes -> True, AxesOrigin -> {-\[Pi]/2, -1}, AxesLabel -> {"\[Phi]", "z"}]

Out[7]=

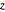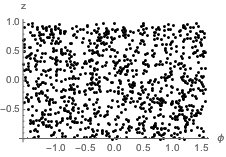
Проверьте гипотезу о том, что совместное распределение 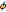и 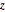является равномерным.

In[8]:=

DistributionFitTest[Transpose[{\[Phi], z}], UniformDistribution[{{-Pi/2, Pi/2}, {-1, 1}}], "TestConclusion"]

Out[8]=