Распределение Трейси-Видома: Новое в системе Wolfram Language 11

Распределение Трейси-Видома

Распределение Трейси-Видома является допредельным распределением нормированного собственного значения случайной матрицы, принадлежащей гауссову ансамблю. Оно также присутствует в различных дисциплинах, таких как проблемы счёта, модели случайного роста, фазовые переходы и т.д. и даёт точные прогнозы.

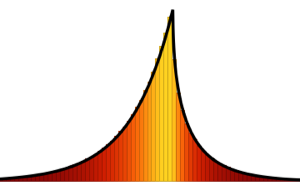
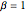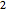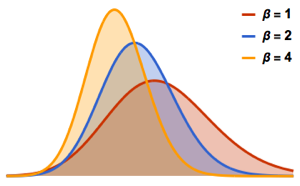
Распределение Трейси-Видома состоит из трёх классов , и 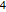. Каждый класс соответствует различным гауссовым ансамблям; ознакомьтесь с соответствующими функциями плотности распределения.

код на языке Wolfram Language целиком

In[1]:=

Plot[Table[
   PDF[TracyWidomDistribution[\[Beta]], x], {\[Beta], {1, 2, 4}}] // 
  Evaluate, {x, -5, 2}, Filling -> Axis, 
 PlotLegends -> {"\[Beta] = 1", "\[Beta] = 2", "\[Beta] = 4"}, 
 ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[1]=

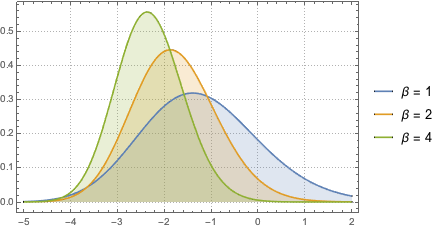
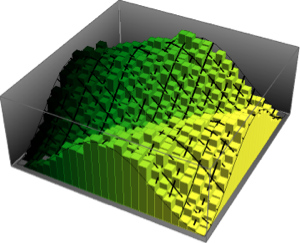
Используйте MatrixPropertyDistribution для представления самого большого нормированного собственного значения матрицы из ГУА.

In[2]:=

ev\[ScriptCapitalD][2, n_] := 
 MatrixPropertyDistribution[(Max[Eigenvalues[x]] - 2 Sqrt[n]) n^(1/6),
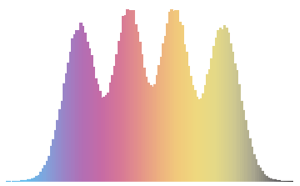
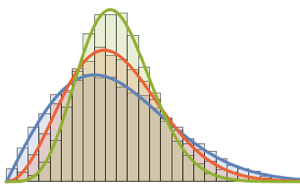
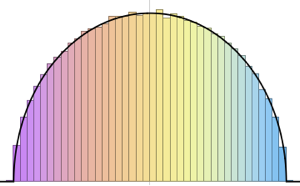
   x \[Distributed] GaussianUnitaryMatrixDistribution[n]]

Сделайте выборку из распределения и сравните гистограмму с функцией плотности распределения.

In[3]:=

sample = RandomVariate[ev\[ScriptCapitalD][2, 250], 2000];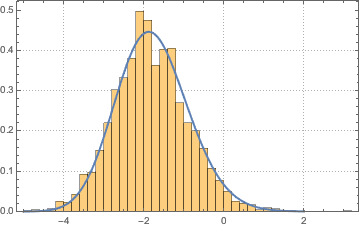

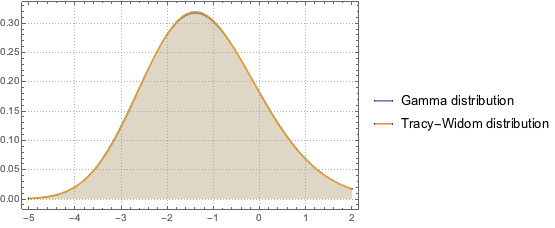
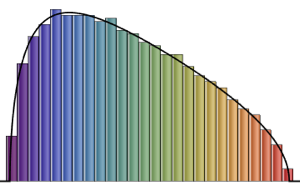
код на языке Wolfram Language целиком

In[4]:=

Show[Histogram[sample, {0.2}, PDF, PlotTheme -> "Detailed"], 
 Plot[PDF[TracyWidomDistribution[2], x ], {x, -5, 2}, 
  PlotStyle -> Thick, PlotTheme -> "Detailed", PlotLegends -> None], 
 ImageSize -> Medium]

Out[4]=

Распределение Трейси-Видома может приближённо описываться гамма-распределением в центральной области.

In[5]:=

gdist = GammaDistribution[k, s, 1, a];
PDF[gdist, x]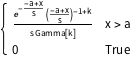

Out[5]=

Приблизьте гамма-распределение к распределению Трейси-Видома при 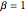путём согласования первых трёх моментов.

In[6]:=

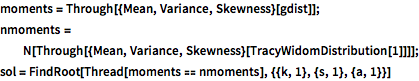
moments = Through[{Mean, Variance, Skewness}[gdist]];
nmoments = 
  N[Through[{Mean, Variance, Skewness}[TracyWidomDistribution[1]]]];
sol = FindRoot[Thread[moments == nmoments], {{k, 1}, {s, 1}, {a, 1}}]

Out[6]=

Сравните функции плотности распределения.

код на языке Wolfram Language целиком

In[7]:=

Plot[{PDF[gdist /. sol, x], PDF[TracyWidomDistribution[1], x]} // 
  Evaluate, {x, -5, 2}, 
 PlotLegends -> {"Gamma distribution", "Tracy-Widom distribution"}, 
 Filling -> Axis, PlotTheme -> "Detailed", ImageSize -> Medium]

Out[7]=