Распределение и обратное распределение Уишарта

Распределение Уишарта - это распределение ковариационной матрицы с выборкой, полученной из независимых многомерных случайных векторов. Оно является обобщением 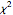(хи-квадрат) распределения в многочисленных измерениях. Распределение формируется естественным образом в многомерном статистическом анализе, таком как регрессия, ковариантность и др.

Сгенерируйте случайную положительную определённую матрицу для использования в качестве параметров для распределения Уишарта.

In[1]:=

\[CapitalSigma] = DiagonalMatrix[RandomReal[10, 5]];

Матрицы из распределения Уишарта симметричны и положительно определены. »

In[2]:=

dist = WishartMatrixDistribution[30, \[CapitalSigma]]; mat = RandomVariate[dist];

In[3]:=

SymmetricMatrixQ[mat] && PositiveDefiniteMatrixQ[mat]

Out[3]=

Обратное распределение Уишарта - это распределение обратных матриц из распределения Уишарта. »

In[4]:=

invdist = InverseWishartMatrixDistribution[30, Inverse[\[CapitalSigma]]]; invmat = RandomVariate[invdist];

Матрицы из обратного распределения Уишарта симметричны и положительно определены.

In[5]:=

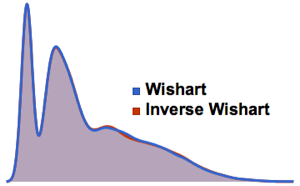
SymmetricMatrixQ[invmat] && PositiveDefiniteMatrixQ[invmat]

Out[5]=

Сравните распределение собственных значений для матриц из распределения и обратного распределения Уишарта.

In[6]:=

eigs = Flatten[ RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] dist], 10^4]]; inveigs = Flatten[RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x]^-1, x \[Distributed] invdist], 10^4]];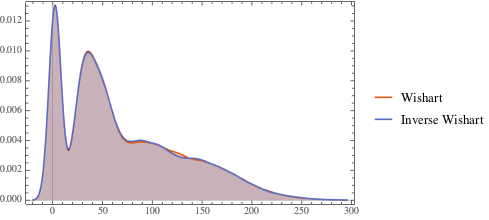

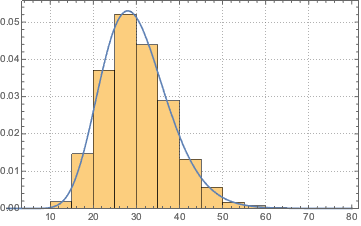
In[7]:=

SmoothHistogram[{eigs, inveigs}, PlotLegends -> {"Wishart", "Inverse Wishart"}, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Scientific"]

Out[7]=

Для любого ненулевого вектора 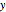и матрицы Уишарта 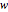со шкалой матрицы 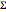, статистические 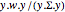имеют 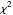(хи-квадрат) распределение.

In[8]:=

y = #/Sqrt[#.\[CapitalSigma].#] &[RandomReal[1, 5]]; data = RandomVariate[ MatrixPropertyDistribution[y.w.y, w \[Distributed] WishartMatrixDistribution[30, \[CapitalSigma]]], 10^4];

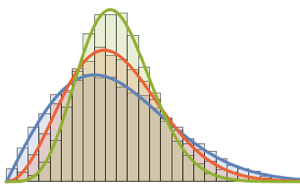
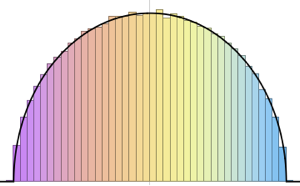
In[9]:=

Show[Histogram[data, Automatic, PDF, PlotTheme -> "Detailed"], Plot[PDF[ChiSquareDistribution[30], x], {x, 0, 80}], ImageSize -> Medium]

Out[9]=