Спектральная плотность матрицы

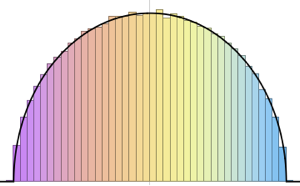
Совместная спектральная плотность многих матричных распределений имеет соответствующую универсальную предельную форму. Для эрмитовых случайных матриц с независимыми элементами эта форма определяется полукруговым законом Вигнера.

Для гауссовых ансамблей, нормированная спектральная плотность матриц имеет закрытую форму измерения конечных матриц, относящyюся к собственным функциям квантового гармонического осциллятора.

Используйте MatrixPropertyDistribution для представления нормированного спектра гауссова унитарного ансамбля и представьте выражение закрытого вида для его совместной спектральной плотности.

In[1]:=

scaledSpectrum\[ScriptCapitalD][n_] := MatrixPropertyDistribution[ Eigenvalues[\[Lambda]]/(2 Sqrt[n]), \[Lambda] \[Distributed] GaussianUnitaryMatrixDistribution[n]];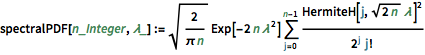

In[2]:=

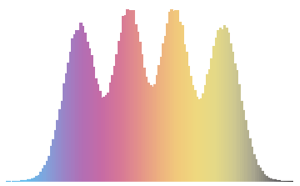
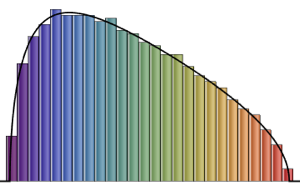
spectralPDF[n_Integer, \[Lambda]_] := Sqrt[2/(\[Pi] n)] Exp[-2 n \[Lambda]^2] \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 0\), \(n - 1\)] \*FractionBox[ SuperscriptBox[\(HermiteH[j, \*SqrtBox[\(2\ n\)]\ \[Lambda]]\), \(2\)], \( \*SuperscriptBox[\(2\), \(j\)]\ \(j!\)\)]\)

Для маленького матричного измерения существует характерный шаблон осциллятора, чьё число максимумa плотности равно размеру матрицы.

In[3]:=

scaledSpectra = Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][#], 10^5]] & /@ {3, 4, 5};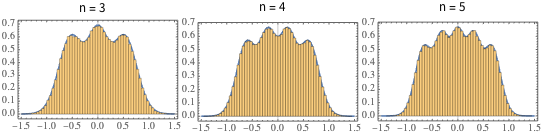

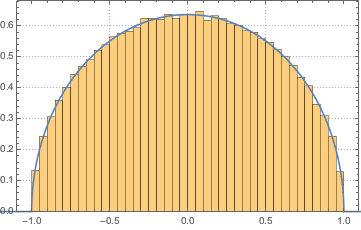
In[4]:=

Row@MapThread[ Show[Plot[spectralPDF[#1, x], {x, -1.5, 1.5}, PlotTheme -> "Scientific", PlotStyle -> ColorData[97, 1], PlotLegends -> Placed["n = " <> ToString@#1, Above]], Histogram[#2, {0.05}, PDF]] &, {{3, 4, 5}, scaledSpectra}]

Out[4]=

В пределах большого измерения плотность стремится к WignerSemicircleDistribution.

In[5]:=

n = 250; scaledSpectrum = Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][n], 10^2]];

In[6]:=

Show[Histogram[scaledSpectrum, {0.05}, PDF, PlotTheme -> "Detailed"], Plot[PDF[WignerSemicircleDistribution[1], x], {x, -1.5, 1.5}, Exclusions -> None, PlotTheme -> "Scientific", PlotLegends -> None, PlotStyle -> ColorData[97, 1]], ImageSize -> Medium]

Out[6]=