Самые длинные возрастающие подпоследовательности
Число перестановок 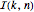 элементов
элементов 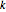 , в которых самая длинная возрастающая подпоследовательность, имеющая предельную длину
, в которых самая длинная возрастающая подпоследовательность, имеющая предельную длину  , может быть вычислена путём нахождения среднего значения
, может быть вычислена путём нахождения среднего значения 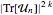 , где
, где 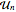 являются матрицами, полученными из CircularUnitaryMatrixDistribution размера массива
являются матрицами, полученными из CircularUnitaryMatrixDistribution размера массива  .
.
In[1]:=
{k, n} = {6, 2};Определите распределение матричных свойств и рассчитайте среднее значение.
In[2]:=

\[ScriptCapitalD] =
MatrixPropertyDistribution[Abs[Tr[\[ScriptCapitalU]]]^(
2 k), \[ScriptCapitalU] \[Distributed]
CircularUnitaryMatrixDistribution[n]];
N[Mean[\[ScriptCapitalD]]]Out[2]=
Сравните с прямым подсчётом.
In[3]:=
Count[Permutations[Range[k]],
perm_ /; Length[LongestOrderedSequence[perm]] <= n]Out[3]=
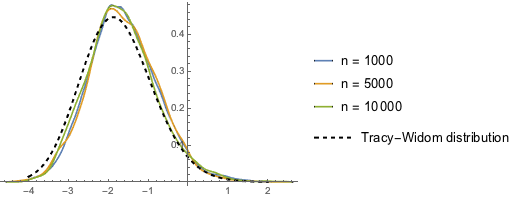
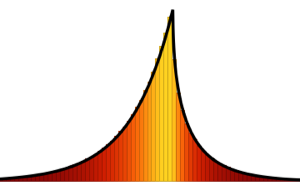
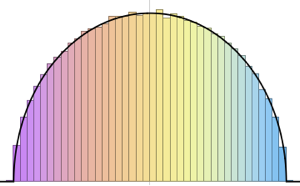
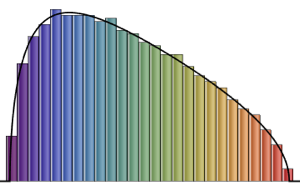
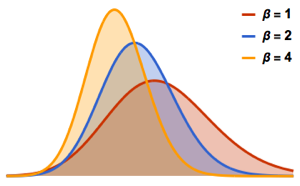
Для 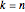 распределение нормированных длин самых длинных возрастающих подпоследовательностей случайных перестановок стремится к распределению Трейси-Видома с
распределение нормированных длин самых длинных возрастающих подпоследовательностей случайных перестановок стремится к распределению Трейси-Видома с 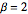 .
.
In[4]:=

sample[n_] :=
1/n^(1/6) (Table[
Length[LongestOrderedSequence[
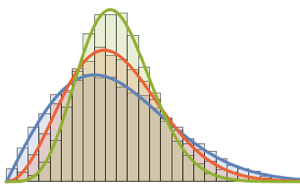
RandomSample[Range[n]]]], {2000}] - 2.0 Sqrt[n]);Сравните сглаженную гистограмму выборочных нормированных длин для возрастающих измерений с функцией распределения плотности распределения Трейси-Видома.
код на языке Wolfram Language целиком
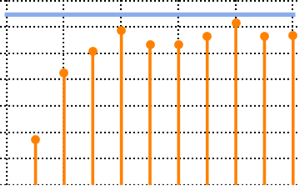
Out[5]=