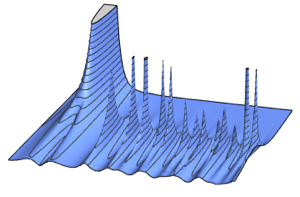
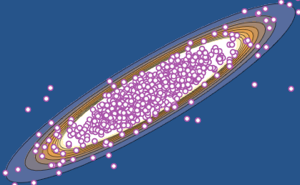
Кулоновский газ Дайсона: Новое в системе Wolfram Language 11

Кулоновский газ Дайсона

Совместное распределение собственных значений матрицы, следующей CircularOrthogonalMatrixDistribution, является равным распределению Больтцмана кулоновского газа Дайсона на окружности с инверсной температурой 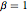. Определите средний гамильтониан (без кинетических параметров) на частицу.

In[1]:=

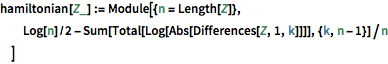
hamiltonian[Z_] := Module[{n = Length[Z]},
  Log[n]/2 - Sum[Total[Log[Abs[Differences[Z, 1, k]]]], {k, n - 1}]/n
  ]

Определите распределение гамильтониана.

In[2]:=

h\[ScriptCapitalD] = 
  MatrixPropertyDistribution[hamiltonian[Eigenvalues[x]], 
   x \[Distributed] CircularOrthogonalMatrixDistribution[n]];

Рассчитайте пример среднего значения гамильтониана для систем различного размера.

In[3]:=

means = Table[{n, Mean[RandomVariate[h\[ScriptCapitalD], 1000]]}, {n, 
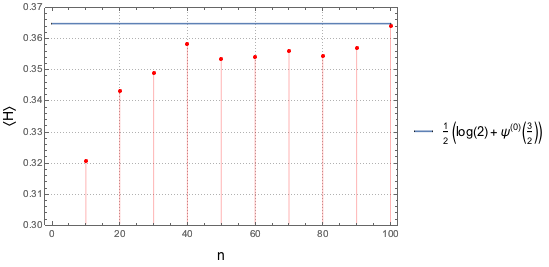
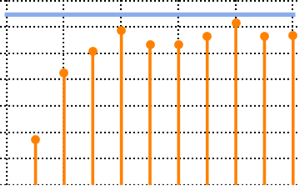
    10, 100, 10}];

Графически изобразите примеры средних значений и сравните их с термодинамическим пределом.

код на языке Wolfram Language целиком

In[4]:=

Show[ListPlot[means, PlotStyle -> {Red, PointSize[Medium]}, 
  Filling -> Axis, PlotRange -> {0.3, 0.37}, 
  FrameLabel -> {Style["n", Black, 14], 
    Style["\[LeftAngleBracket]H\[RightAngleBracket]", Black, 14]}, 
  PlotTheme -> "Detailed"], 
 Plot[1/2 (Log[2] + PolyGamma[0, 3/2]), {x, 0, 100}, 
  PlotTheme -> "Detailed"]]

Out[4]=