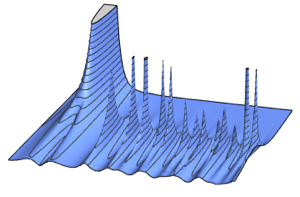
Свойства матричных распределений

Статистика меньшей размерности, полученная из случайных матриц играет значимую роль в характеристике матричных ансамблей. В различных ограничивающих ситуациях распределения данных статистик распадаются на различные классы универсальностей. MatrixPropertyDistribution обеспечивает удобный доступ для выборки и расчёта численного приблизительного значения этих полученных свойств.

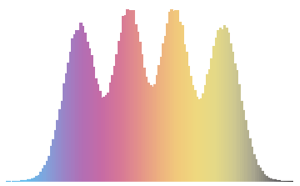
Отберите два самых больших собственных значения из гауссова унитарного ансамбля.

In[1]:=

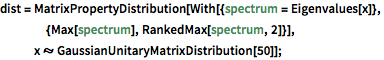
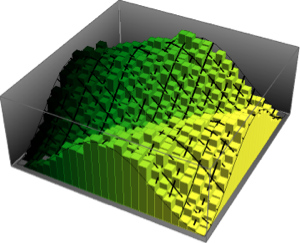
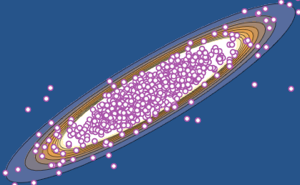
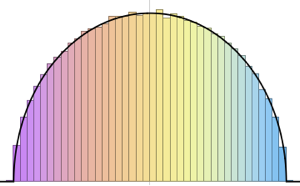
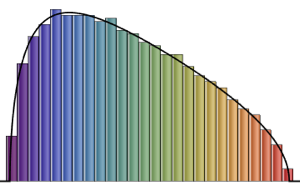
dist = MatrixPropertyDistribution[With[{spectrum = Eigenvalues[x]}, {Max[spectrum], RankedMax[spectrum, 2]}], x \[Distributed] GaussianUnitaryMatrixDistribution[50]];

In[2]:=

RandomVariate[dist]

Out[2]=

Визуализируйте совместное распределение двух самых больших собственных значений, основанных на результате выборки.

In[3]:=

sample = RandomVariate[dist, 10^4];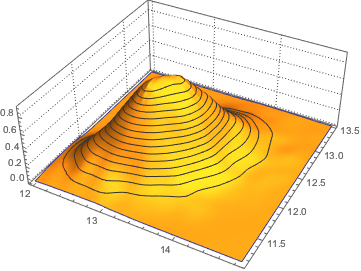

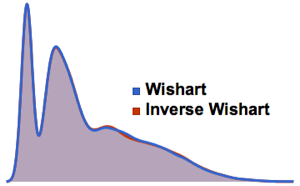
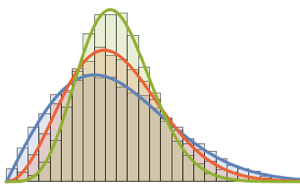
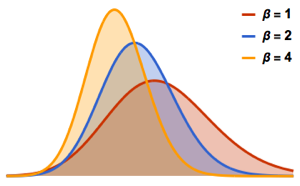
In[4]:=

SmoothHistogram3D[sample, "Scott", "PDF", PlotTheme -> "Detailed", ImageSize -> Medium]

Out[4]=

Отберите определитель матриц из гауссова ортогонального ансамбля и сравните эмпирическое распределение с выражением в замкнутой форме.

In[5]:=

dist = MatrixPropertyDistribution[Det[x], x \[Distributed] GaussianOrthogonalMatrixDistribution[2]]; dets = RandomVariate[dist, 10^6];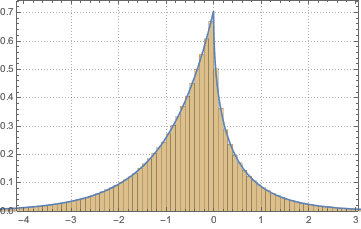

In[6]:=

empirical = Histogram[dets, {0.1}, PDF, PlotTheme -> "Detailed", ImageSize -> Medium]; detpdf[y_] := 1/Sqrt[2] Exp[ y] Piecewise[{{Erfc[Sqrt[2 y]], y >= 0}, {1, y < 0}}]; analytical = Plot[detpdf[y], {y, -5, 4}, Exclusions -> None, PlotLegends -> None, PlotTheme -> "Detailed", ImageSize -> Medium, Filling -> Axis]; Show[empirical, analytical]

Out[6]=

Приблизительно определите среднее значение определителя с помощью выборки по методу Монте-Карло и сравните его с действительным значением.

In[7]:=

{N@Mean[dist], Integrate[x detpdf[x], {x, -Infinity, Infinity}]}

Out[7]=