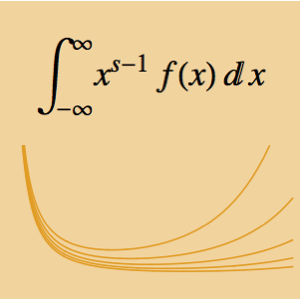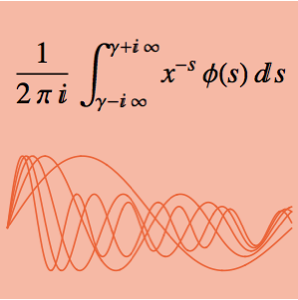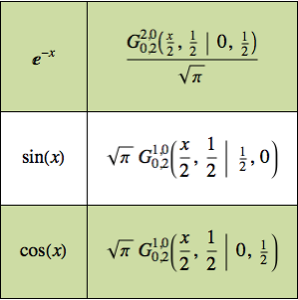Resolva um desafio da SIAM (Sociedade para a Matemática Aplicada e Industrial)
A integral 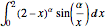 depende do parâmetro α. Ache o valor de α que está entre 0 e 5 e maximize a integral. A integral dada pode ser considerada como uma convolução de Mellin de duas funções.
depende do parâmetro α. Ache o valor de α que está entre 0 e 5 e maximize a integral. A integral dada pode ser considerada como uma convolução de Mellin de duas funções.
In[1]:=
f[x_] := x (2 - x)^\[Alpha] UnitBox[(x - 1)/2]In[2]:=
g[x_] := Sin[x]Calcule a convolução de Mellin de f[x] and g[x].
In[3]:=
(mc = MellinConvolve[f[x], g[x], x, \[Alpha]]) // TraditionalFormOut[3]//TraditionalForm=
Compare com o resultado dado por Integrate.
In[4]:=
Integrate[(2 - x)^\[Alpha] Sin[\[Alpha]/x], {x, 0, 2},
Assumptions -> \[Alpha] > 0] // TraditionalFormOut[4]//TraditionalForm=
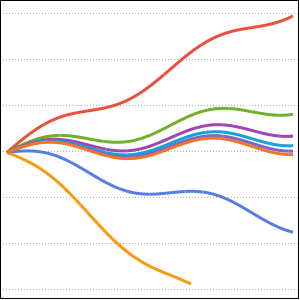
Faça o gráfico da integral como uma função de α.
In[5]:=
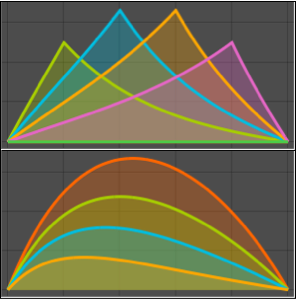
Plot[mc // Evaluate, {\[Alpha], 0, 4.99}, PlotStyle -> Red]Out[5]=
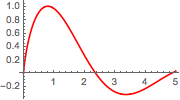
Calcule o argumento que maximize a integral em 0≤α≤5 usando FindArgMax.
In[6]:=
N[FindArgMax[mc, {\[Alpha], 1}, WorkingPrecision -> 100][[1]], 20]Out[6]=