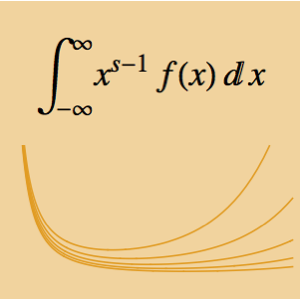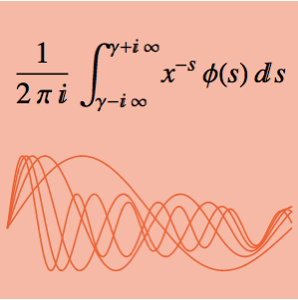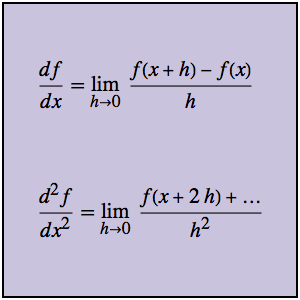SIAM 챌린지 문제 풀이
적분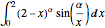 
는 매개변수 α에 의존합니다. 0에서 5 사이의 α 값을 구하고, 적분을 극대화합니다. 주어진 적분은 두 함수의 멜린 합성곱이라 고려할 수 있습니다.
In[1]:=
f[x_] := x (2 - x)^\[Alpha] UnitBox[(x - 1)/2]In[2]:=
g[x_] := Sin[x]f[x]와 g[x]의 멜린 합성곱을 계산합니다.
In[3]:=
(mc = MellinConvolve[f[x], g[x], x, \[Alpha]]) // TraditionalFormOut[3]//TraditionalForm=
Integrate에 의해 주어진 결과를 비교합니다.
In[4]:=
Integrate[(2 - x)^\[Alpha] Sin[\[Alpha]/x], {x, 0, 2},
Assumptions -> \[Alpha] > 0] // TraditionalFormOut[4]//TraditionalForm=
적분을 α의 함수로 플롯합니다.
In[5]:=
Plot[mc // Evaluate, {\[Alpha], 0, 4.99}, PlotStyle -> Red]Out[5]=
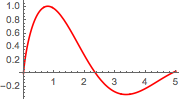
FindArgMax를 사용하여 0≤α≤5에서 적분을 극대화하는 인수를 계산합니다.
In[6]:=
N[FindArgMax[mc, {\[Alpha], 1}, WorkingPrecision -> 100][[1]], 20]Out[6]=
