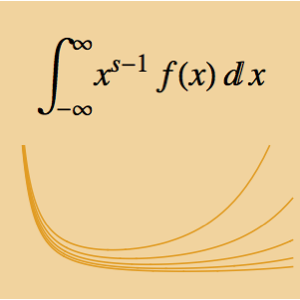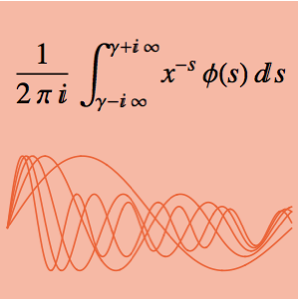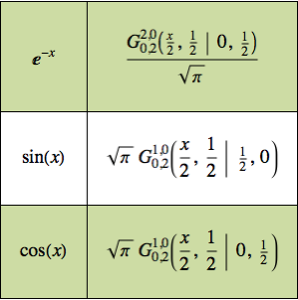Résolvez un problème de défi SIAM
L'intégrale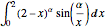 
dépend du paramètre de α. Trouvez la valeur de 
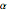qui se trouve entre 
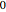et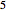 
et maximise l'intégrale. L'intégrale peut être considérée comme une convolution de Mellin de deux fonctions.
In[1]:=
f[x_] := x (2 - x)^\[Alpha] UnitBox[(x - 1)/2]In[2]:=
g[x_] := Sin[x]Calculez la convolution de Mellin de f[x] et de g[x].
In[3]:=
(mc = MellinConvolve[f[x], g[x], x, \[Alpha]]) // TraditionalFormOut[3]//TraditionalForm=
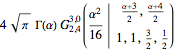
Comparez avec le résultat donné par Integrate.
In[4]:=
Integrate[(2 - x)^\[Alpha] Sin[\[Alpha]/x], {x, 0, 2},
Assumptions -> \[Alpha] > 0] // TraditionalFormOut[4]//TraditionalForm=
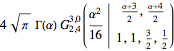
Tracez l'intégrale comme une fonction de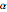 
.
In[5]:=
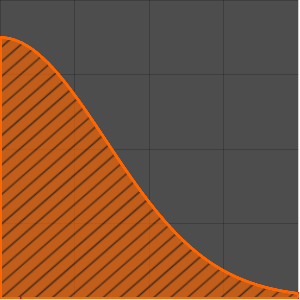
Plot[mc // Evaluate, {\[Alpha], 0, 4.99}, PlotStyle -> Red]Out[5]=
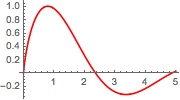
Calculez l'argument qui maximise l'intégrale dans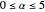 
en utilisant FindArgMax.
In[6]:=
N[FindArgMax[mc, {\[Alpha], 1}, WorkingPrecision -> 100][[1]], 20]Out[6]=
