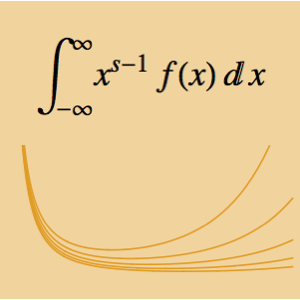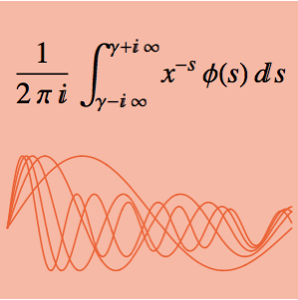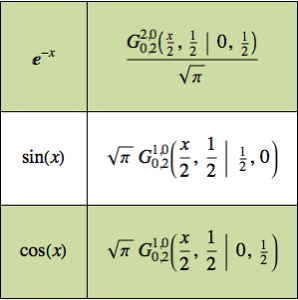SIAMチャレンジ問題を解く

積分 はパラメータ α に依存する．0から5の間の α の値を求め，積分を最大化する．与えられた積分は，2つの関数のメリンたたみ込みと考えることができる．

In[1]:=

f[x_] := x (2 - x)^\[Alpha] UnitBox[(x - 1)/2]

In[2]:=

g[x_] := Sin[x]

f[x]とg[x]のメリンたたみ込みを計算する．

In[3]:=

(mc = MellinConvolve[f[x], g[x], x, \[Alpha]]) // TraditionalForm

Out[3]//TraditionalForm=

Integrateによって与えられた結果を比較する．

In[4]:=

Integrate[(2 - x)^\[Alpha] Sin[\[Alpha]/x], {x, 0, 2}, Assumptions -> \[Alpha] > 0] // TraditionalForm

Out[4]//TraditionalForm=

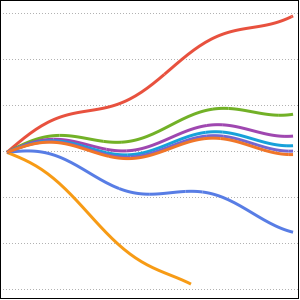
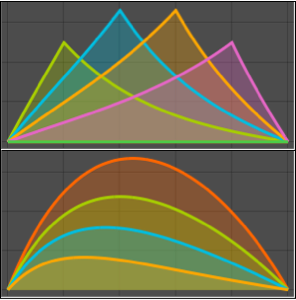
積分を α の関数としてプロットする．

In[5]:=

Plot[mc // Evaluate, {\[Alpha], 0, 4.99}, PlotStyle -> Red]

Out[5]=

FindArgMaxを使って，で積分を最大化する引数を計算する．

In[6]:=

N[FindArgMax[mc, {\[Alpha], 1}, WorkingPrecision -> 100][[1]], 20]

Out[6]=