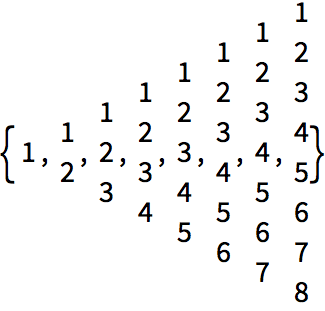WOLFRAM

An Elementary Introduction to the Wolfram Language
6Construcción de tablas
Se han visto ya algunas maneras de formar listas en Wolfram Language. Se puede simplemente escribirlas manualmente. Se puede utilizar Range. Se pueden usar funciones tales como IntegerDigits. Pero una manera muy común y flexible para formarlas es mediante el uso de la función Table.
En su forma más simple,Table construye una lista con el mismo elemento repetido un número especificado de veces.
Forme una lista que tenga el 5 repetido 10 veces:
In[1]:=
Click for copyable input
Out[1]=
Esto construye una lista con x repetido 10 veces:
In[2]:=
Click for copyable input
Out[2]=
También se pueden repetir listas:
In[3]:=
Click for copyable input
Out[3]=
Y, de hecho, cualquier otra cosa; a continuación aparece una lista de 3 gráficos circulares idénticas:
In[4]:=
Click for copyable input
Out[4]=
Pero, ¿y si se deseara formar una tabla cuyos elementos no sean idénticos? Esto se logra introduciendo una variable, para usarla haciendo una iteración sobre ella.
Itere sobre n para formar una lista donde n tome valores hasta el 5:
In[5]:=
Click for copyable input
Out[5]=
Esto funciona de la siguiente manera. Para formar el primer elemento de la lista, se toma n igual a 1, así que a[n] es a[1]. Para el segundo elemento, se toma n igual a 2, así que a[n] es a[2], etc. A n se le llama variable porque cambia de valor a medida que se van construyendo los diferentes elementos de la lista.
Construya una tabla que produzca el valor de n + 1 cuando n toma valores del 1 al 10:
In[6]:=
Click for copyable input
Out[6]=
Forme una tabla de los 10 primeros cuadrados:
In[7]:=
Click for copyable input
Out[7]=
Con Table se pueden formar tablas de cosas cualesquiera.
He aquí una tabla de listas sucesivamente más grandes, producidas con Range:
In[8]:=
Click for copyable input
Out[8]=
Aquí se muestra, en una columna, cada una de las listas producidas anteriormente:
In[9]:=
Click for copyable input
Out[9]=
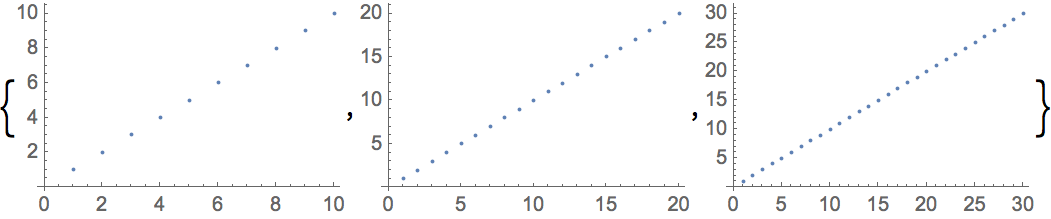
Ahora se muestra una tabla de gráficos de listas sucesivamente más grandes:
In[10]:=
Click for copyable input
Out[10]=
Aquí aparecen gráficos circulares con un número de sectores cada vez mayor :
In[11]:=
Click for copyable input
Out[11]=
Hasta ahora se ha venido usando n como nombre de la variable utilizada, que es algo muy habitual. Pero puede utilizarse para eso cualquier letra minúscula que se desee, o cualquier combinación de letras. Lo importante es que siempre se use el mismo nombre dondequiera que aparezca la variable en cuestión.
expt es un nombre perfectamente adecuado para una variable:
In[12]:=
Click for copyable input
Out[12]=
Abajo se usa x como nombre de la variable y aparece en varios lugares:
In[13]:=
Click for copyable input
Out[13]=
En Table[f[n],{n,5}], n toma los valores 1, 2, 3, 4, 5. En cambio, Table[f[n],{n,3,5}] indica que hay que comenzar en 3: 3, 4, 5.
Esto genera una tabla donde n varía del 1 al 10:
In[14]:=
Click for copyable input
Out[14]=
Esto produce una tabla donde n varía del 4 al 10:
In[15]:=
Click for copyable input
Out[15]=
Aquí se indica que la n debe recorrer los valores del 4 al 10, de 2 en 2:
In[16]:=
Click for copyable input
Out[16]=
Wolfram Language hace hincapié en la consistencia así que, por ejemplo, Range actúa igual que Table en lo que se refiere a valores iniciales e incrementos.
Genere la secuencia de números del 4 al 10:
In[17]:=
Click for copyable input
Out[17]=
Genere la secuencia de números del 4 al 10, de 2 en 2:
In[18]:=
Click for copyable input
Out[18]=
Vaya del 0 al 1 en incrementos de 0.1:
In[19]:=
Click for copyable input
Out[19]=
Suele haber varias maneras de hacer la misma cosa en Wolfram Language. Así, por ejemplo, se muestra cómo Table y Range pueden producir gráficos idénticos.
Genere una lista y represéntela gráficamente:
In[20]:=
Click for copyable input
Out[20]=
Se obtiene el mismo resultado haciendo algo de aritmética con la secuencia de valores:
In[21]:=
Click for copyable input
Out[21]=
Table siempre calcula por separado cada elemento de la lista que genera, y esto puede observarse al utilizar RandomInteger dentro de Table.
Esto genera 20 enteros aleatorios independientes entre 0 y 10:
In[22]:=
Click for copyable input
Out[22]=
De hecho, esta lista podría generarse directamente con RandomInteger.
Otra forma de generar 20 enteros aleatorios entre 0 y 10:
In[23]:=
Click for copyable input
Out[23]=
Vocabulario
Table[x,5] lista de 5 copias de x
Table[f[n],{n,10}] lista de valores de f[n] donde n varía hasta el 10
Table[f[n],{n,2,10}] lista de valores donde n varía desde el 2 hasta el 10
Table[f[n],{n,2,10,4}] lista de valores donde n varía del 2 hasta el 10, de 4 en 4
Range[5,10] lista de los números del 5 al 10
Range[10,20,2] lista de los números del 10 al 20, de 2 en 2
RandomInteger[10,20] lista de 20 enteros aleatorios entre 0 y 10
1.1Forme una lista con el número 1000 repetido 5 veces. »
Salida esperada:
Out[]=
1.1Cree una lista de los valores de n^3 donde n va del 10 al 20. »
Salida esperada:
Out[]=
1.1Construya un gráfico con los 20 primeros cuadrados sobre la recta numérica. »
Salida esperada:
Out[]=
1.1Forme una lista de las diferencias entre n^3 y n^2 para n menor o igual a 10. »
Salida esperada:
Out[]=
1.1Construya una lista de los números pares (2, 4, 6, ...) hasta el 20. »
Salida esperada:
Out[]=
1.1Forme una lista de los números impares (1, 3, 5, ...) hasta el 100. »
Salida esperada:
Out[]=
1.1Cree una lista de los cuadrados de los números pares hasta el 100. »
Salida esperada:
Out[]=
1.1Cree la lista {-3, -2, -1, 0, 1, 2} utilizando Range. »
Salida esperada:
Out[]=
1.1Use Table para obtener el mismo resultado que Range[10]. »
Salida esperada:
Out[]=
1.1Construya un diagrama de barras de los 10 primeros cuadrados. »
Salida esperada:
Out[]=
1.1Construya una lista con los números n hasta el 20, donde cada elemento sea una columna de los valores de n, n^2 y n^3. »
Salida esperada:
Out[]=
1.1Forme una tabla de listas de los dígitos de los 10 primeros cuadrados. »
Salida esperada:
Out[]=
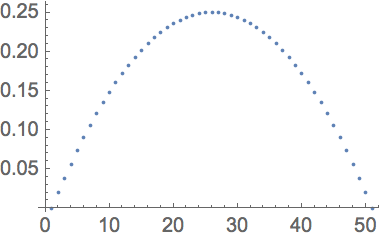
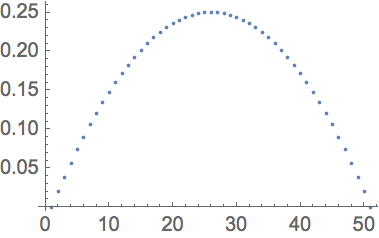
1.1Construya el gráfico, con los puntos unidos, de la longitud de la secuencia de los dígitos de cada uno de los 100 primeros cuadrados. »
Salida esperada:
Out[]=
1.1Forme una tabla del primer dígito de cada uno de los 20 primeros cuadrados. »
Salida esperada:
Out[]=
1.1Haga el gráfico de los primeros dígitos de los 100 primeros cuadrados. »
Salida esperada:
Out[]=
1.1Presente un gráfico, con los puntos unidos, del último dígito de cada uno de los 100 primeros cuadrados. »
Salida esperada:
Out[]=
1.1Cree un gráfico, con los puntos unidos, del primer dígito de cada uno de los primeros 100 múltiplos de 3. »
Salida esperada:
Out[]=
1.1Produzca un gráfico, con los puntos unidos, de la suma de los dígitos de cada número hasta el 200. »
Salida esperada:
Out[]=
1.1Construya una gráfica, con los puntos unidos, de la suma de los dígitos para cada uno de los 100 primeros cuadrados. »
Salida esperada:
Out[]=
1.1Obtenga un gráfico, con los puntos sobre la recta numérica, de los números 1/n, con n variando de 1 a 20. »
Salida esperada:
Out[]=
1.1Produzca un gráfico, con los puntos unidos, de una lista de enteros aleatorios, donde el n-ésimo entero esté entre 0 y n. »
Muestra de salida esperada:
Out[]=
Preguntas y respuestas
¿Qué significa la lista {...} (lista) en Table[n^2, {n, 5}]?
Una lista siempre es una forma de reunir cosas. En este caso lo que se reúne es la variable n con su secuencia de valores hasta el 5. En Wolfram Language, esta forma de usar una lista se llama especificación del iterador.
¿Por qué es necesaria la lista {...} in Table[n^2, {n, 5}]?
Porque de esa manera se puede generalizar fácilmente a los arreglos multidimensionales, como en Table[x^2-y^2, {x, 5}, {y, 5}].
¿Qué restricciones hay para los nombres de variables?
Pueden ser cualquier secuencia de letras y números, pero no pueden comenzar con un número. Además, para evitar confusiones con las funciones nativas de Wolfram Language, no deben comenzar con mayúscula.
¿Por qué hay que poner nombre a una variable, si los nombres no importan?
¡Buena pregunta! En la Sección 26 se verá cómo evitar el uso del nombre de las variables. Esto es más elegante, aunque un poco más abstracto de lo que hasta ahora se viene haciendo con Table.
¿Puede Range trabajar con números negativos?
Desde luego. Range[-2, 2] produce {-2, -1, 0, 1, 2}. Range[2, -2] produce {}, por Range[2, -2, -1] produce {2, 1, 0, -1, -2}.
Notas técnicas
  • En el caso de que se especifiquen incrementos que no se ajusten bien al tramo que se haya determinado, Range y Table llegarán hasta donde los lleven los incrementos y, potencialmente, se detendrán antes del límite superior. (Así Range[1, 6, 2] produce {1, 3, 5}, deteniéndose en 5, y no en 6.)
  • Usar una forma tal como Table[x, 20] requiere tener activa, cuando menos, la Versión 10.2 de Wolfram Language. En versiones anteriores esto tendría que especificarse comoTable[x, {20}].
    • Para explorar más
    La función Table en Wolfram Language »
     
    Download Notebook Version
    en