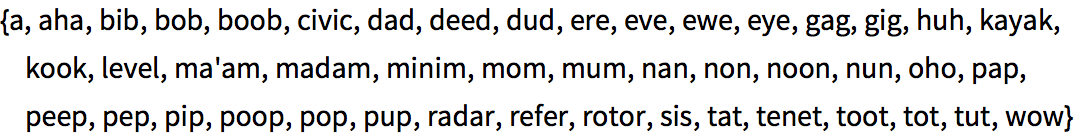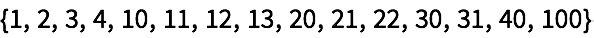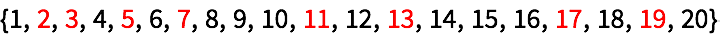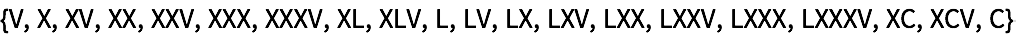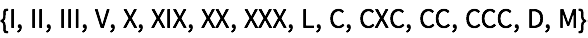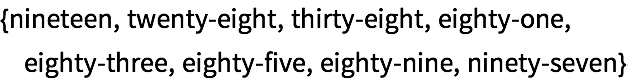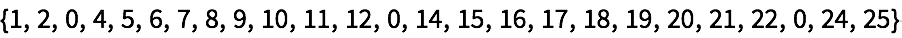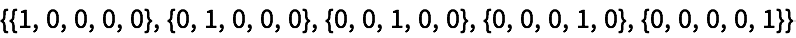An Elementary Introduction to the Wolfram Language
28Pruebas y condicionales
¿Es 2+2 igual a 4? Se le pregunta a Wolfram Language.
Compruebe si 2+2 es igual a 4:
In[1]:=
Click for copyable input
Out[1]=
No es de sorprender que al comprobar si 2+2 es igual a 4, el resultado sea True (que significa verdadero en inglés).
Puede comprobarse también si 2×2 es mayor que 5. Para ese propósito se usa >.
Compruebe si 2×2 es mayor que 5:
In[2]:=
Click for copyable input
Out[2]=
La función If permite elegir un resultado cuando una comprobación da True, y otro cuando da False.
Puesto que la comprobación da True, el resultado del If es x:
In[3]:=
Click for copyable input
Out[3]=
Si se usa una función pura con /@, puede aplicarse un If a cada elemento de una lista.
Si un elemento es menor que 4, hacerlo x, de lo contrario hacerlo y:
In[4]:=
Click for copyable input
Out[4]=
Puede hacerse la comprobación para menor o igual usando ≤, lo que se escribe como <=.
Si un elemento es menor o igual a 4, hágalo x; de lo contrario, hágalo y:
In[5]:=
Click for copyable input
Out[5]=
En lo que sigue, un elemento se hace x solo si es igual a 4:
In[6]:=
Click for copyable input
Out[6]=
Puede hacerse la comprobación de que dos cosas no sean iguales usando ≠, lo que se escribe como !=.
Si un elemento no es igual a 4, hacerlo x; de lo contrario, hacerlo y:
In[7]:=
Click for copyable input
Out[7]=
A veces es útil seleccionar aquellos elementos de una lista que satisfagan un criterio. Esto se hace usando Select, estableciendo dicha comprobación en términos de una función pura.
Seleccione los elementos de la lista que sean mayores que 3:
In[8]:=
Click for copyable input
Out[8]=
Seleccione los elementos que estén entre 2 y 5:
In[9]:=
Click for copyable input
Out[9]=
Además de las comparaciones de tamaño tales como <, > y ==, Wolfram Language incluye muchos otros tipos de pruebas. Algunos ejemplos son EvenQ y OddQ, que comprueban si un número es par o impar. (La “Q” indica que una función está formulando una pregunta).
4 es un número par:
In[10]:=
Click for copyable input
Out[10]=
Seleccione de la lista los números pares:
In[11]:=
Click for copyable input
Out[11]=
En este caso no es necesario que la función pura se haga explícita:
In[12]:=
Click for copyable input
Out[12]=
IntegerQ comprueba si algo es un entero; PrimeQ comprueba si un número es primo.
Seleccione los números primos:
In[13]:=
Click for copyable input
Out[13]=
A veces se necesita combinar comprobaciones. && representa “y”, || representa “o” y ! representa “no”.
Seleccione los elementos de la lista que sean a la vez pares y mayores que 2:
In[14]:=
Click for copyable input
Out[14]=
Seleccione los elementos que sean pares o mayores que 4:
In[15]:=
Click for copyable input
Out[15]=
Seleccione los elementos que no sean pares o mayores que 4:
In[16]:=
Click for copyable input
Out[16]=
Hay muchas otras “funciones Q” que formulan preguntas sobre diversos tipos de cosas. LetterQ comprueba si una cadena de caracteres está compuesta solo de letras.
El espacio entre letras no es una letra, ni tampoco lo es “!”:
In[17]:=
Click for copyable input
Out[17]=
Convierta una cadena en una lista de caracteres, y compruebe cuáles de ellos son letras:
In[18]:=
Click for copyable input
Out[18]=
Seleccione los caracteres que sean letras:
In[19]:=
Click for copyable input
Out[19]=
Seleccione las letras que estén después de la posición 10 en el alfabeto inglés:
In[20]:=
Click for copyable input
Out[20]=
Puede usarse Select para encontrar palabras en inglés que sean palíndromos, esto es, que se lean igual si se invierte el orden de sus letras.
In[21]:=
Click for copyable input
Out[21]=
MemberQ comprueba si alguna cosa aparece como un elemento de una lista o está contenido en ella.
5 aparece en la lista {1, 3, 5, 7}:
In[22]:=
Click for copyable input
Out[22]=
Seleccione los números entre 1 y 100 cuyas secuencias de dígitos contengan el 2:
In[23]:=
Click for copyable input
Out[23]=
ImageInstanceQ es una comprobación basada en el aprendizaje automático que comprueba si una imagen es un caso de algún tipo particular de algo como, por ejemplo, un gato.
Compruebe si una imagen es la de un gato:
In[24]:=
Click for copyable input
Out[24]=
Seleccione las imágenes que sean de gatos:
In[25]:=
Click for copyable input
Out[25]=
He aquí un ejemplo geográfico de Select: encuentre cuáles de las ciudades en una lista se ubican a menos de 3 000 millas de San Francisco.
Seleccione las ciudades cuya distancia a San Francisco sea menor de 3 000 millas:
In[26]:=
Click for copyable input
Out[26]=
Vocabulario
ab comprueba igualdad
a<b comprueba si es menor que
a>b comprueba si es mayor que
a≤b comprueba si es menor o igual
a≥b comprueba si es mayor o igual
If[test,u,v] obtiene el resultado u si test es True y v si es False
Select[lista,f] selecciona los elementos que satisfacen un criterio
EvenQ[x] comprueba si es par
OddQ[x] comprueba si es impar
IntegerQ[x] comprueba si es un entero
PrimeQ[x] comprueba si es un número primo
LetterQ[cadena] comprueba si solo son letras
MemberQ[lista,x] comprueba si x está contenido en lista
ImageInstanceQ[imagen,categoría] comprueba si imagen es un caso de categoría
28.1Compruebe si 123^321 es mayor que 456^123. »
Salida esperada:
Out[]=
28.2Obtenga una lista de los números hasta el 100 cuyos dígitos sumen menos de 5. »
Salida esperada:
Out[]=
28.3Haga una lista de los 20 primeros enteros, coloreando con rojo los que sean primos. »
Salida esperada:
Out[]=
28.4Encuentre las palabras en WordList[ ] que comiencen y terminen con la letra “p”. »
Muestra de salida esperada:
Out[]=
28.5Haga una lista de los 100 primeros primos, conservando aquellos cuyo último dígito sea menor que 3. »
Salida esperada:
Out[]=
28.6Encuentre los números romanos hasta el 100 que no contengan “I”. »
Salida esperada:
Out[]=
Salida esperada:
Out[]=
Salida esperada:
Out[]=
28.9Obtenga la lista de las palabras en el artículo de Wikipedia “words”, cuyo número de caracteres sea mayor de 15. »
Muestra de salida esperada:
Out[]=
Salida esperada:
Out[]=
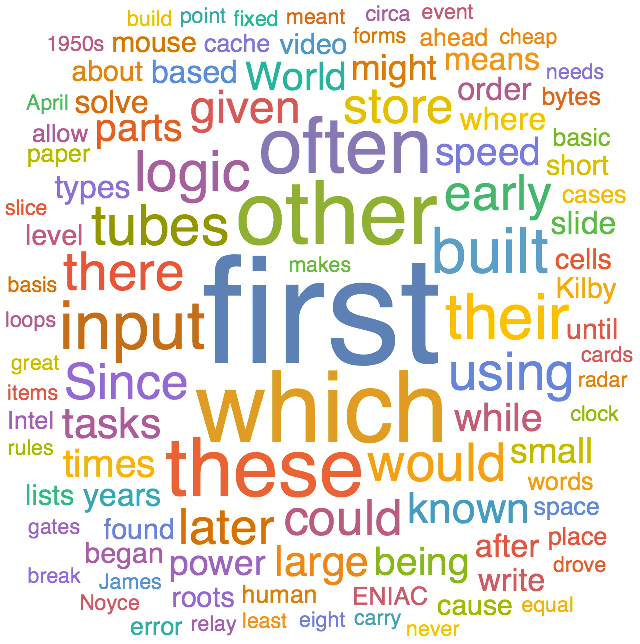
28.11Cree la nube de las palabras que tengan 5 letras en el artículo de Wikipedia sobre “computers”. »
Muestra de salida esperada:
Out[]=
28.12Encuentre las palabras en WordList[ ] cuyas 3 primeras letras sean las mismas que sus 3 últimas en orden inverso, pero tales que la cadena completa de sus caracteres no sea un palíndromo. »
Muestra de salida esperada:
Out[]=
28.13Encuentre las palabras de 10 letras en WordList[ ] donde el total de los valores obtenidos con LetterNumber sea 100. »
Muestra de salida esperada:
Out[]=
+28.1Haga una lista de los enteros hasta el 25, donde cada entero que termine en 3 se reemplace por 0. »
Salida esperada:
Out[]=
+28.2Use Table e If para hacer un arreglo de 5×5 que tenga 1 en su diagonal principal, y 0 fuera de ahí.  »
Salida esperada:
Out[]=
+28.3Haga una lista de los números hasta el 1000 que sean a la vez iguales a 1 mod 7 y a 1 mod 8. »
Salida esperada:
Out[]=
+28.4Haga una lista de los números hasta el 100, en la que los múltiplos de 3 se reemplacen por Black, los que sean múltiplos de 5 se reemplacen por White y los que sean a la vez múltiplos de 3 y de 5 se reemplacen por Red. »
Salida esperada:
Out[]=
+28.5Use Select para obtener la lista de los planetas cuya masa sea mayor que la de la Tierra. »
Salida esperada:
Out[]=
+28.6Haga un gráfico de arreglo 50×50 donde haya un cuadrado negro en la posición i, j si Mod[i, j]==0. »
Salida esperada:
Out[]=
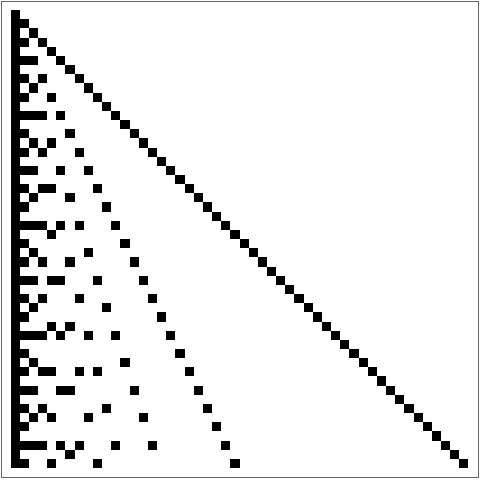
+28.7Haga un gráfico de arreglo de 100×100, donde un cuadrado sea negro si los dos valores de sus posiciones x y y no contienen un 5. »
Salida esperada:
Out[]=
Preguntas y respuestas
¿Por qué la igualdad se comprueba con == y no con =?
Porque en Wolfram Language = significa otra cosa. Si por error se usa = en vez de , se obtendrán resultados muy extraños. (= es para asignar valores a variables.) Para evitar posibles confusiones, suele leerse == como “doble signo de igual”.
¿Por qué “and” se escribe como &&, y no como &?
Porque & significa otra cosa en Wolfram Language. Por ejemplo, se usa para indicar dónde termina una función pura.
¿Cómo se interpretan ==, >, &&, etc. ?
== es Equal, ≠ (!=) es Unequal, > es Greater, ≥ es GreaterEqual, < es Less, && es And, || es Or y ! es Not.
¿En qué casos se requiere usar paréntesis al usar &&, ||, etc.?
Hay un orden en las operaciones que es directamente análogo al de la aritmética. && es como ×, || es como +, y ! es como −. Entonces, !p&&q significa “(no p) y q”; !(p&&q) significa “no (p y q)”.
¿Qué tienen de especial las funciones “Q”?
Hacen una pregunta que normalmente tiene como respuesta True o False.
¿Qué otras funciones “Q” existen?
NumberQ, StringContainsQ, BusinessDayQ y ConnectedGraphQ, entre otras.
¿Hay alguna forma mejor que Select para encontrar entidades del mundo real que tengan alguna propiedad dada?
Sí. Se pueden hacer cosas como Entity["Country", "Population"GreaterThan[]] para encontrar “entidades implícitas”, y usar luego EntityList para obtener listas explícitas de entidades.
Notas técnicas
  • True y False se llaman típicamente booleanos en las ciencias de la computación (por George Boole, a mediados de los años 1800s). Las expresiones con &&, ||, etc. se suelen llamar expresiones booleanas.
  • En Wolfram Language, True y False son símbolos, y no están representadas por 1 y 0, como sucede en muchos otros lenguajes de computación.
  • If se suele llamar una condicional. En If[test, then, else], el then y else no se calculan a menos que test diga que la condición se cumple.
  • PalindromeQ prueba directamente si una cadena de caracteres forma un palíndromo.
  • En Wolfram Language, x es un símbolo (ver la Sección 33) que puede representar cualquier cosa, así que x==1 es simplemente una ecuación, que no es inmediatamente True o False. x===1 (“triple igual”) prueba si x es “lo mismo” que 1, y puesto que no lo es, da False.
Para explorar más
Guía para funciones que aplican pruebas en Wolfram Language »
Guía para computación Booleana en Wolfram Language »
 
Download Notebook Version
en