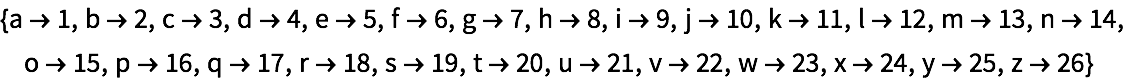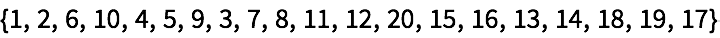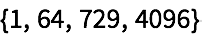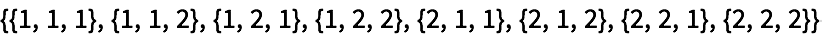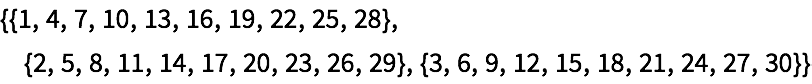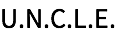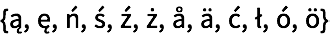| 30 | Reorganización de listas |
Muchas veces se quiere reorganizar una lista que se haya generado en algún proceso, antes de poder utilizarla en otro. Por ejemplo, puede tenerse una lista de pares que se necesite convertir a un par de listas, o viceversa.
Transponga una lista de pares para convertirla en un par de listas:
Transponga de nuevo el par de listas para obtener una lista de pares:
Thread es una operaci
ón estrechamente relacionada con la anterior, que sirve, entre otras, para generar una entrada para
Graph.
“Enhebrar
” a trav
és de los elementos de dos listas:
Partition toma una lista y la particiona en bloques de un tama
ño especificado.
Particione una lista con 12 elementos en bloques de tamaño 3:
Particione una lista de caracteres y mostrarlos en una rejilla:
Si no se especifica lo contrario,
Partition descompone una lista en bloques que no se traslapen. Sin embargo, puede pedirse que la lista se descomponga en bloques que permitan un traslape mediante un desplazamiento especificado en la lista.
Particione una lista en bloques de tama
ño 3, con un desplazamiento de 1:
Particione una lista de caracteres en bloques con un desplazamiento de 1:
En vez de lo anterior, use un desplazamiento de 2:
Partition toma una lista y la descompone en sublistas.
Flatten “aplana
” las sublistas.
Forme una lista de las listas de los dígitos de enteros consecutivos:
Obtenga la versión aplanada:
Produzca un gráfico con la secuencia de dígitos:
Normalmente,
Flatten aplana en todos los niveles de una lista. Sin embargo, muchas veces se querr
ía aplanar, por ejemplo, solo un nivel de la lista. Aqu
í se forma una tabla de 4
×4, donde cada elemento es, a su vez, una lista.
Forme una lista de listas de listas:
Aplane todo el resultado:
Aplane solo un nivel de la lista:
ArrayFlatten es una generalizaci
ón de
Flatten, que toma arreglos de arreglos y los aplana para hacer arreglos individuales.
Aquí se genera una estructura con anidación profunda que resulta difícil de comprender:
ArrayFlatten la convierte en una estructura un poco m
ás f
ácil de entender:
Con
ArrayPlot, es considerablemente m
ás sencillo darse cuenta de lo que est
á sucediendo:
Genere un
patrón de Sierpinski fractal con 8 niveles de anidaci
ón:
Hay muchas otras maneras de reorganizar listas. Por ejemplo,
Split subdivide una lista en secuencias de elementos id
énticos.
Subdivida una lista en secuencias de elementos idénticos consecutivos:
Gather, por otro lado, agrupa los elementos que sean id
énticos, dondequiera que
éstos aparezcan.
Agrupe en listas los elementos idénticos:
GatherBy agrupa los elementos seg
ún el resultado de aplicar una funci
ón a cada uno. Ahora, se usa
LetterQ, de modo tal que agrupa por separado los caracteres que son letras y los que no lo son.
Agrupe los caracteres según sean letras o no lo sean:
SortBy ordena seg
ún el resultado de aplicar una funci
ón.
Sort normalmente ordena las listas cortas antes de las m
ás largas:
Ahora se le pide a
SortBy que haga el ordenamiento de acuerdo al primer elemento de cada lista:
Sort ordena una lista.
Union, adem
ás, elimina los elementos repetidos.
Encuentre en una lista todos los elementos que sean distintos:
Se puede usar
Union para encontrar la
“uni
ón
” de los elementos que aparezcan en cualesquiera de varias listas.
Obtenga la lista de todos los elementos que aparezcan en cualquiera de las listas:
Encuentre los elementos que sean comunes a todas las listas:
Encuentre los elementos que est
én en la primera de las listas, pero no en la segunda:
Encuentre las letras que aparezcan en cualquiera de los alfabetos ingl
és, sueco o turco:
Las letras que aparecen en el sueco, pero no en el inglés:
Otra de las muchas funciones que se pueden aplicar a las listas es
Riffle, que intercala cosas entre los elementos sucesivos de una lista.
Intercale x entre los elementos de una lista:
Intercale -- entre una lista de caracteres:
Junte todo lo anterior en una sola lista de caracteres:
Las funciones tales como
Partition sirven para tomar una lista y descomponerla en sublistas. En vez de eso, a veces se parte de una colecci
ón de elementos para formar listas con ellos.
Permutations obtiene todos los ordenamientos posibles, o
permutaciones, de una lista.
Genere una lista de los 3!=3×2×1=6 ordenamientos posibles de 3 elementos:
Genere todos los 2
3=8 subconjuntos que se pueden formar con los elementos de una lista de 3:
Tuples toma una lista de elementos y genera todas las combinaciones posibles de un n
úmero dado de dichos elementos.
Genere una lista de todas las ternas posibles de rojo y verde:
RandomChoice sirve para hacer una elecci
ón aleatoria a partir de los elementos de una lista.
Haga una elección aleatoria a partir de los elementos de una lista:
Haga una lista de 20 elecciones aleatorias:
Haga 5 listas de 3 elecciones aleatorias:
RandomSample obtiene una muestra aleatoria de elementos de una lista, sin seleccionar m
ás de una vez ning
ún elemento.
Elija 20 elementos en el tramo de 1 a 100, sin que aparezca ningún elemento repetido:
Si no se indica cuántos elementos se han de elegir, se obtiene un ordenamiento aleatorio de la lista completa:
| Transpose[lista] | | transpone las listas interior y exterior |
| Thread[lista1lista2] | | enhebra a través de elementos de listas |
| Partition[lista,n] | | particiona en bloques de tamaño n |
| Flatten[lista] | | aplana todas las sublistas |
| Flatten[lista,k] | | aplana k niveles de las sublistas |
| ArrayFlatten[lista] | | aplana arreglos de arreglos |
| Split[lista] | | separa en secuencias de elementos idénticos |
| Gather[lista] | | agrupa en listas los elementos idénticos |
| GatherBy[lista,f] | | agrupa de acuerdo con el resultado de aplicar f |
| SortBy[lista,f] | | ordena de acuerdo con el resultado de aplicar f |
| Riffle[lista,x] | | intercala x entre los elementos de lista |
| Union[lista] | | los elementos diferentes en lista |
| Union[lista1,lista2, ...] | | los elementos que aparecen en cualquiera de las listas |
| Intersection[lista1,lista2, ...] | | los elementos que aparecen en todas las listas |
| Complement[lista1,lista2] | | los elementos que aparecen en lista1 pero no en lista2 |
| Permutations[lista] | | todas las permutaciones (ordenamientos) posibles |
| Subsets[lista] | | todos los subconjuntos posibles |
| Tuples[lista,n] | | todas las combinaciones posibles de n elementos |
| RandomChoice[lista] | | elige aleatoriamente dentro de una lista |
| RandomChoice[lista,n] | | n elecciones aleatorias |
| RandomSample[lista,n] | | n muestras aleatorias sin repeticiones |
| RandomSample[lista] | | ordenamiento aleatorio de una lista |
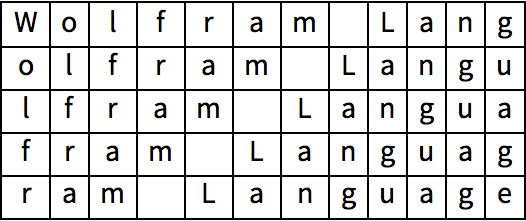
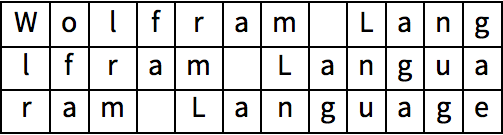
30.1Use
Thread para formar una lista de reglas que liguen cada letra del alfabeto ingl
és con su posici
ón en el alfabeto.
»
30.2Haga una rejilla de 4
×6 con las 24 primeras letras del alfabeto ingl
és.
»
30.3Forme una rejilla con los d
ígitos en 2^1000, con 50 d
ígitos en cada rengl
ón y con un marco en todos los casos.
»
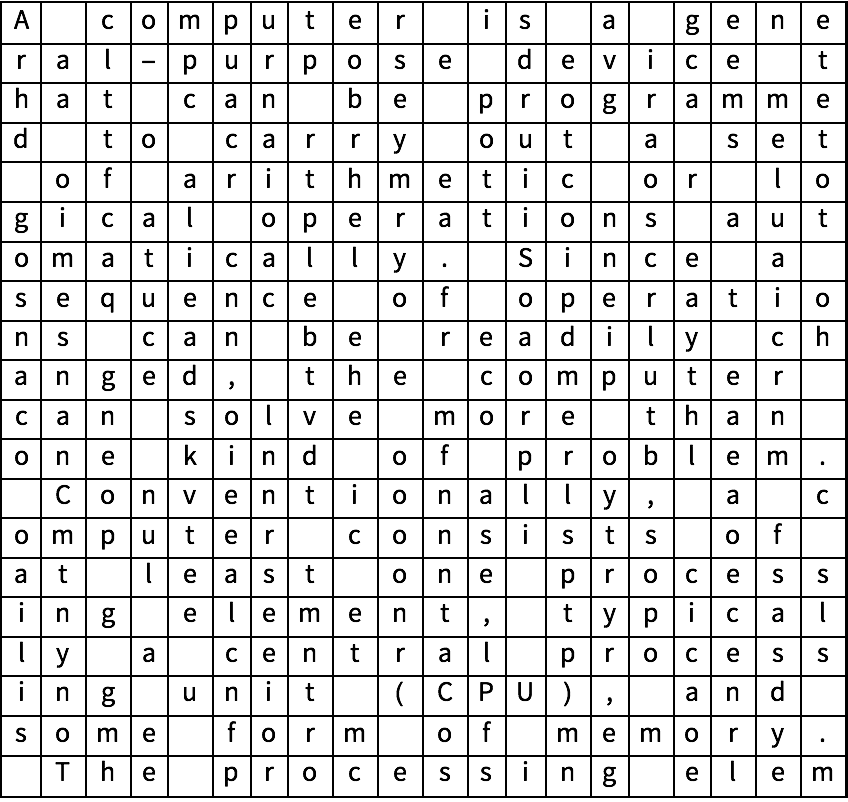
30.4Forme una rejilla con los 400 primeros caracteres del art
ículo
“computers
” en Wikipedia, con 20 caracteres por rengl
ón y con un marco en todos los casos.
»
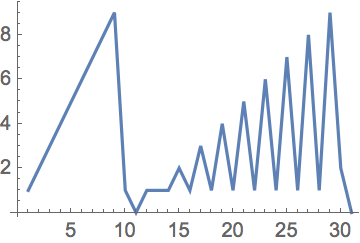
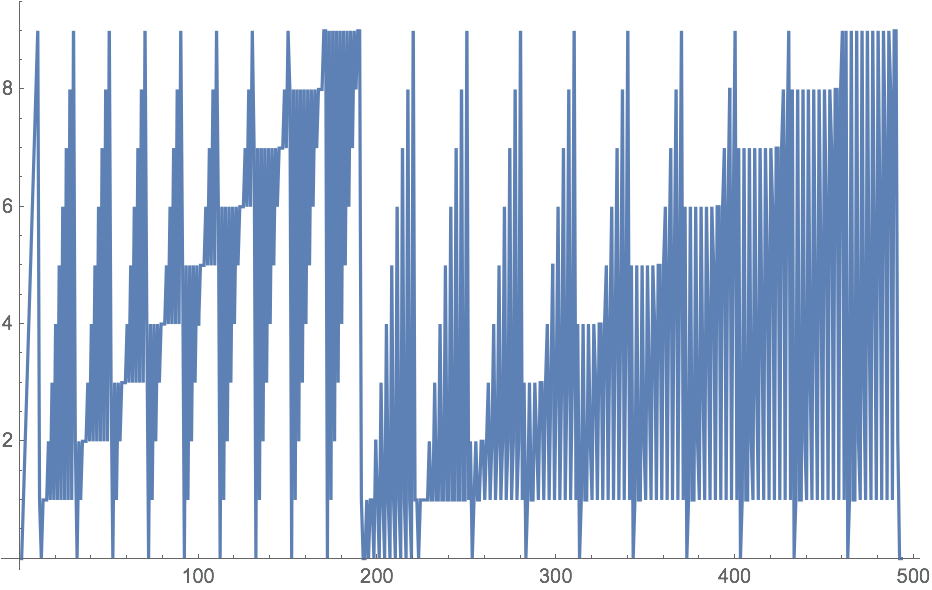
30.5Obtenga un gr
áfico con los puntos unidos de la lista aplanada de los d
ígitos de los n
úmeros del 0 al 200
(la secuencia de Champernowne).
»
30.6Efect
úe 4 pasos del an
álogo
“esponja de Menger” del patr
ón de Sierpinski fractal del texto, pero con un
kernel de la forma
{{#, #, #}, {#, 0, #}, {#, #, #}}.
»
30.7Encuentre las
ternas pitagóricas que tengan solo enteros, seleccionando
{x, y, Sqrt[x^2+y^2]}, con
x y
y del 1 hasta el 20.
»
30.8Encuentre las longitudes m
ás largas entre las secuencias de d
ígitos id
énticos en
2^n, con
n hasta 100.
»
30.9Tome los nombres de los enteros hasta el 100, y agr
úpelos en sublistas con acuerdo a sus letras iniciales.
»
30.10Ordene las 50 primeras palabras en
WordList[ ] seg
ún la
última letra.
»
30.11Haga una lista de los 20 primeros cuadrados, ordenada por sus primeros d
ígitos.
»
30.12Ordene los enteros hasta el 20, seg
ún las longitudes de sus nombres en ingl
és.
»
30.13Obtenga una muestra aleatoria de 20 palabras de
WordList[ ], y agr
úpelas en sublistas, de acuerdo con el n
úmero de sus caracteres.
»
30.14Encuentre las letras que aparecen en el alfabeto ucraniano, pero no en el ruso.
»
30.15Use
Intersection para encontrar los n
úmeros que aparecen tanto en los 100 primeros cuadrados como en los 100 primeros cubos.
»
30.16Encuentre la lista de los pa
íses que pertenecen tanto a la OTAN como al G8.
»
30.17Haga una rejilla donde aparezcan en columnas consecutivas todas las permutaciones posibles de los n
úmeros 1 al 4.
»
30.18Haga una lista de todas las diferentes cadenas de caracteres que pueden obtenerse permutando los caracteres en
“hello
”.
»
30.19Obtenga un gr
áfico de arreglo de la secuencia de tuplas de tama
ño 5, con el 0 y el 1.
»
30.20Genere una lista de 10 secuencias aleatorias de 5 letras del alfabeto ingl
és.
»
30.21Encuentre una forma m
ás sencilla para
Flatten[Table[{i, j, k}, {i, 2}, {j, 2}, {k, 2}], 2].
»
+30.1Produzca un gr
áfico de arreglo con los n
úmeros de las letras en los 1000 primeros caracteres del art
ículo
“computers
” en Wikipedia, con 30 letras en cada rengl
ón.
»
+30.2Agrupe los enteros hasta el 30 en listas basadas en sus valores m
ódulo 3.
»
+30.3Agrupe las 50 primeras potencias de 2 de acuerdo con el valor de sus
últimos d
ígitos.
»
+30.4Obtenga un gr
áfico con los puntos unidos con el resultado de ordenar los n
úmeros del
−10 al +10, seg
ún sus valores absolutos.
»
+30.5Produzca un gr
áfico con los puntos unidos de los 200 primeros cuadrados, ordenados por sus d
ígitos iniciales.
»
+30.6Produzca el gr
áfico con los puntos unidos de los enteros hasta el 200, ordenados seg
ún las longitudes de sus nombres en ingl
és.
»
+30.7Obtenga una muestra aleatoria de 25 palabras de
WordList[].
»
+30.8Intercale puntos en la cadena de caracteres
“UNCLE
” para obtener
“U.N.C.L.E.
”.
»
+30.9Encuentre las letras que aparecen en sueco o en polaco, pero no en ingl
és.
»
+30.10Encuentre los pa
íses que pertenecen a la World Health Organization pero no a las Naciones Unidas.
»
+30.11Haga la lista de todas las mezclas de dos de los colores rojo, verde y azul.
»
+30.12Haga una lista de gr
áficos de arreglo, cada uno con 50 renglones y tama
ño de imagen 50, de las tuplas sucesivas de tama
ño 8, con el 0 y el 1.
»
+30.13Genere 1000 secuencias aleatorias de 4 letras, y hacer la lista de aquellas que aparezcan en
WordList[ ].
»
¿C
ómo funciona
Partition cuando los bloques no encajan perfectamente?
A menos que se indique lo contrario, solo se incluir
án bloques completos, de tal modo que se eliminar
án aquellos elementos que aparezcan solo en bloques incompletos. Sin embargo, si se dice, por ejemplo,
Partition[lista, UpTo[4]], se har
án bloques
hasta de longitud 4, y el
último de ellos podr
ía ser m
ás corto si fuera necesario.
- Transpose puede verse como la transposición de filas y columnas en una matriz.
- ArrayFlatten aplana un arreglo de arreglos para dejar un solo arreglo o, alternativamente, para dejar una matriz de matrices en una sola matriz.
- DeleteDuplicates[lista] hace lo mismo que Union[lista], salvo que no reordena los elementos.