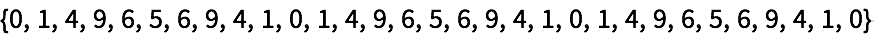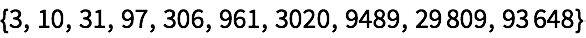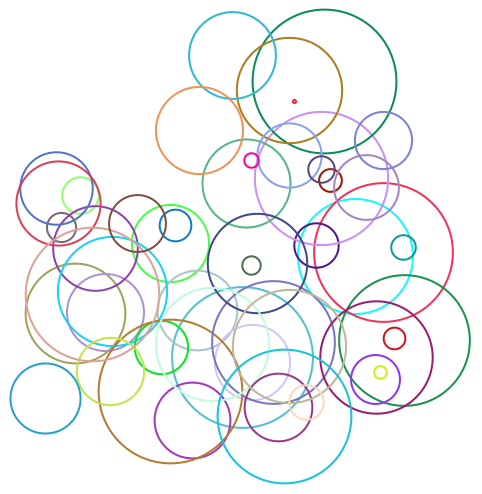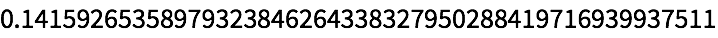Al hacer c
álculos con n
úmeros enteros, Wolfram Language da respuestas exactas. Lo mismo sucede con las fracciones exactas.
Sumar 1/2+1/3 da el resultado exacto en forma de fracción:
Frecuentemente, lo que se desea es una aproximaci
ón num
érica o decimal. Esto se obtiene usando la funci
ón
N (por
“num
érica
”).
Obtenga una respuesta numérica aproximada:
Si en la entrada aparece algún número decimal, Wolfram Language dará automáticamente una respuesta aproximada.
La presencia de un número decimal hace que el resultado sea aproximado:
Es suficiente con poner un punto decimal al final de alguno de los n
úmeros:
Wolfram Language puede trabajar con n
úmeros de cualquier tama
ño, con tal de que quepan en la memoria de la computadora que se est
é usando.
Aquí aparece 2 elevado a la potencia 1000:
Para obtener una aproximación numérica:
Esta forma aproximada est
á dada en
notación científica. Para ingresar algo en notaci
ón cient
ífica puede usarse *^.
Ingrese un número en notación científica:
Aquellos n
úmeros que sean de uso frecuente como
π (pi) est
án ya construidos dentro de Wolfram Language.
Obtenga una aproximación numérica de π:
Wolfram Language puede calcular con
precisión arbitraria y, por ejemplo, puede dar millones de d
ígitos para
π, si se desea.
Calcule 250 dígitos de π:
Existen muchas funciones en Wolfram Language que manejan
números enteros. Hay tambi
én muchas funciones que manejan
números reales (n
úmeros aproximados con decimales). Por ejemplo,
RandomReal, que produce n
úmeros aleatorios reales.
Genere un número aleatorio real en el tramo de 0 a 10:
Genere 5 números aleatorios reales:
Una forma alternativa de pedir 5 números aleatorios reales:
N
úmeros aleatorios reales en el tramo entre 20 y 30:
Wolfram Language contiene una cantidad enorme de funciones matemáticas nativas, desde las muy básicas hasta otras con un alto grado de sofisticación.
Encuentre el n
úmero primo en la posici
ón 100:
Encuentre el número primo en la posición un millón:
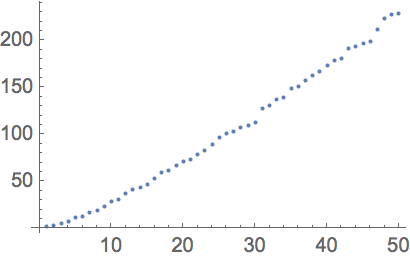
Produzca un gráfico de los primeros 50 primos:
Hay tres funciones muy comunes en situaciones pr
ácticas, que son
Sqrt (ra
íz cuadrada),
Log10 (logaritmo en base 10) y
Log (logaritmo natural).
La raíz cuadrada de 16 es 4:
Si no se pide una aproximación numérica, se obtiene una fórmula exacta:
N produce una aproximaci
ón num
érica:
Los logaritmos son
útiles cuando se manejan n
úmeros con una amplia variabilidad en sus tama
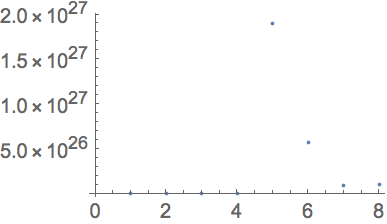
ños. Si se grafican las masas de los planetas,
ListPlot no revela nada sobre los planetas anteriores a J
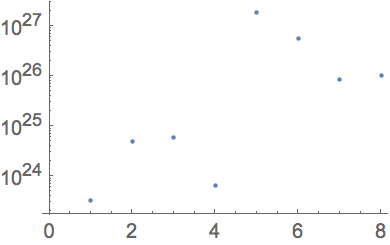
úpiter. Pero
ListLogPlot muestra muy claramente sus tama
ños relativos.
Muestre un gráfico ordinario de las masas de los planetas:
Muestre un gr
áfico en escala logar
ítmica:
Hay unas cuantas funciones m
ás que aparecen frecuentemente en la programaci
ón com
ún. Primero, la funci
ón, casi trivial,
Abs, que encuentra el valor absoluto, o parte positiva, de un n
úmero.
Abs realmente lo que hace es desechar los signos menos:
Enseguida est
á Round, que efect
úa el redondeo al entero m
ás cercano.
Round redondea al entero m
ás cercano:
Otra funci
ón muy
útil es
Mod. Cuando se est
án contando los minutos en una hora, al llegar a 60 se desea comenzar de nuevo desde 0, y eso es lo que hace
Mod.
Calcule una secuencia de números mod 60:
| N[expr] | | aproximación numérica |
| Pi | | el número π (pi)≃3.14 |
| Sqrt[x] | | raíz cuadrada |
| Log10[x] | | logaritmo en base 10 |
| Log[x] | | logaritmo natural (ln) |
| Abs[x] | | valor absoluto (desechar los signos menos) |
| Round[x] | | redondea al entero más cercano |
| Prime[n] | | número primo |
| Mod[x,n] | | módulo (“aritmética del reloj”) |
| RandomReal[max] | | número real aleatorio entre 0 y max |
| RandomReal[max,n] | | lista de n números reales aleatorios |
| ListLogPlot[data] | | produce la gráfica en escala logarítmica |
23.1Encuentre
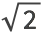
con una precisi
ón de 500 d
ígitos.
»
23.2Genere 10 n
úmeros reales aleatorios entre 0 y 1.
»
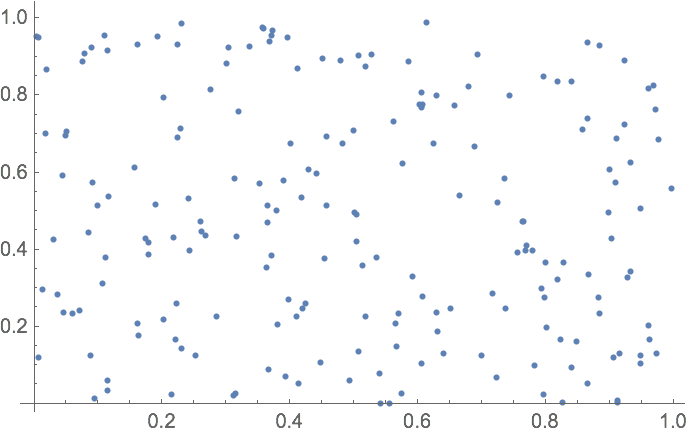
23.3Haga un gr
áfico de 200 puntos con coordenadas reales
x e
y aleatorias entre 0 y 1.
»
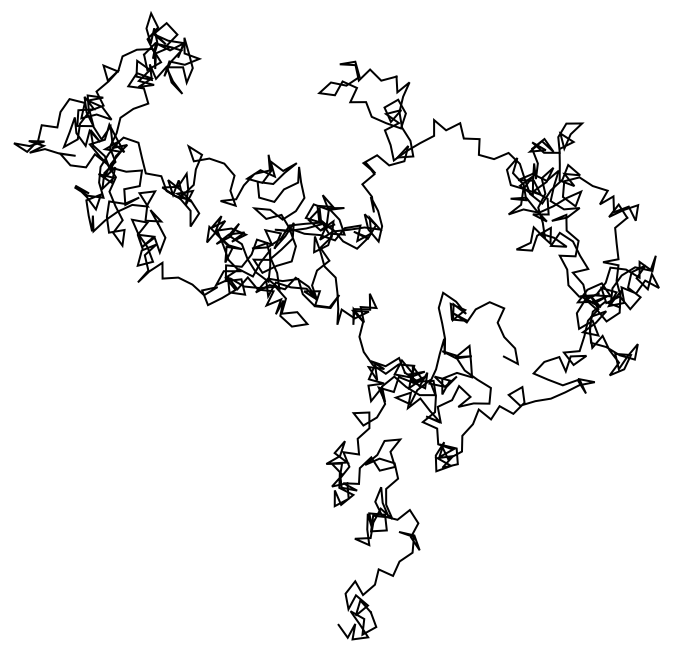
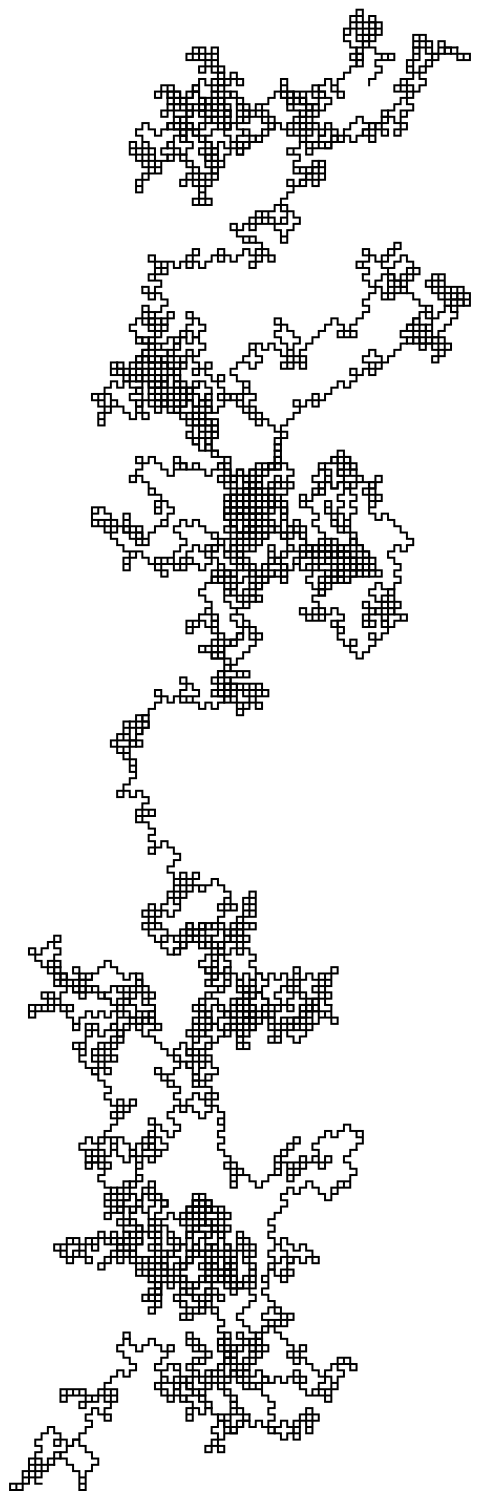
23.4Cree una caminata aleatoria usando
AnglePath y 1000 n
úmeros reales aleatorios entre 0 y 2
π.
»
23.5Haga una tabla de
Mod[n^2, 10] para n de 0 a 30.
»
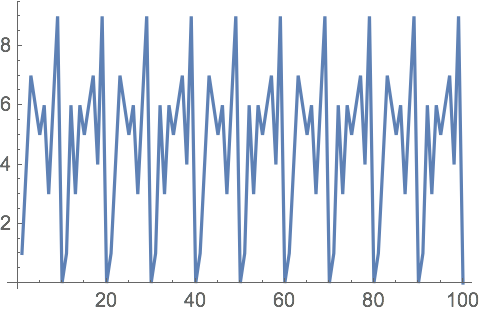
23.6Haga un gr
áfico con los puntos unidos de
Mod[n^n, 10] para
n de 1 a 100.
»
23.7Haga una tabla de las primeras 10 potencias de
π, redondeadas a enteros.
»
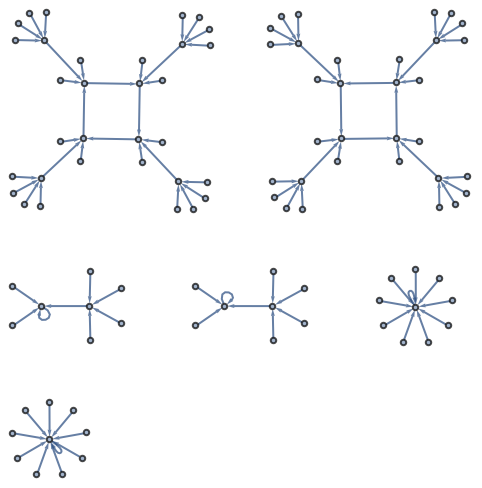
23.8Construya un grafo conectando n con
Mod[n^2, 100] para
n desde 0 a 99.
»
23.9Genere los gr
áficos de 50 c
írculos con coordenadas reales aleatorias de 0 a 10, con radios reales aleatorios de 0 a 2, y de colores aleatorios.
»
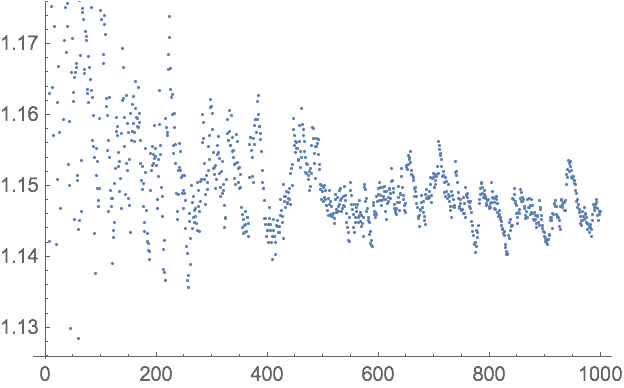
23.10 Presente gr
áficamente el n-
ésimo primo dividido por
n*log(n), para
n del 2 al 1000.
»
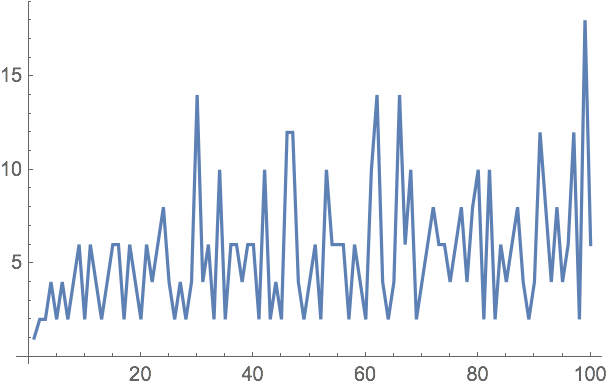
23.11Presente un gr
áfico con los puntos unidos de las diferencias entre primos consecutivos hasta el 100.
»
23.12Genere una secuencia de 20 notas C central (do central), de duraciones aleatorias entre 0 y 0.5 segundos.
»
23.13Genere un gr
áfico de arreglo para
Mod[i, j] con
i y
j hasta 50.
»
23.14Construya una lista de gr
áficos de arreglo de x^y mod n, con n de 2 a 10, para x e y hasta 50.
»
+23.1Use
Round para calcular la parte fraccionaria de
π con 50 d
ígitos.
»
+23.2Encuentre la suma de los primeros 1000 n
úmeros primos.
»
+23.3Construya una lista con los primeros 100 primos m
ódulo 4.
»
+23.4Forme la lista de los primeros 10
000 primos m
ódulo 4, multipl
íquelos por 90
° y cree una trayectoria angular con el resultado.
»
¿Se pueden dar ejemplos de funciones matem
áticas en Wolfram Language?
De las matem
áticas escolares est
ándar, se pueden dar algunos ejemplos tales como
Sin,
Cos,
ArcTan,
Exp, as
í como
GCD,
Factorial,
Fibonacci. De la f
ísica, la ingenier
ía y las matem
áticas superiores, algunos tales como
Gamma (
“funci
ón gamma
”),
BesselJ (
“funci
ón de Bessel
”),
EllipticK (
“integral el
íptica
”),
Zeta (
“funci
ón zeta de Riemann
”),
PrimePi,
EulerPhi. De la estad
ística, algunos otros tales como
Erf,
NormalDistribution,
ChiSquareDistribution. En total, centenares de ellos.
¿Qu
é es la precisi
ón de un n
úmero?
Es el n
úmero total de d
ígitos decimales que aparecen en ese n
úmero.
N[100/3, 5] da
33.333, que tiene una precisi
ón de 5 d
ígitos. El n
úmero
100/3 es exacto;
N[100/3, 5] lo aproxima con una precisi
ón de 5 d
ígitos.
¿Qu
é significa
al final de cada rengl
ón en un n
úmero muy largo?
Indica que el número continúa en el siguiente renglón, como el guión en un texto.
¿Se puede trabajar con n
úmeros en bases diferentes de 10?
S
í. Si hubiera que escribir un n
úmero en base 16, se har
ía como
16^^ffa5. Se encuentran los d
ígitos usando
IntegerDigits[655, 16].
¿Puede Wolfram Language manejar n
úmeros complejos?
Desde luego. El s
ímbolo
I (
“i
” may
úscula) representa la ra
íz cuadrada de
−1.
¿Por qu
é N[1.5/7, 100] no da un resultado con 100 d
ígitos?
Porque 1.5 es un n
úmero aproximado con una precisi
ón mucho menor de 100 d
ígitos. Pero, por ejemplo,
N[15/70, 100] da un n
úmero con una precisi
ón de 100 d
ígitos.
- Wolfram Language efectúa “computación con precisión arbitraria”, es decir, puede conservar tantos dígitos en un número como se quiera.
- Cuando se genera un número con cierta precisión usando N, Wolfram Language llevará automáticamente la cuenta de cómo afecta dicha precisión a los cálculos, de tal modo que uno no tiene que efectuar su propio análisis de los errores de redondeo.
- Al ingresar un número tal como 1.5, se supone que tiene la “precisión de máquina” nativa de los números en la computadora que se esté usando (por lo general, unos 16 dígitos, aunque usualmente solo se muestran 6). Se usa 1.5 `100 para especificar una precisión de 100 dígitos.
- Si se ingresa un número exacto (tal como 4 o 2/3 o Pi), Wolfram Language trata siempre de dar una salida exacta. Pero si la entrada contiene un número aproximado (como 2.3) o, si se usa N, utilizará la aproximación numérica.
- La aproximación numérica es muchas veces crucial para hacer posibles los cálculos en gran escala.
- PrimeQ comprueba si un número es primo (ver la Sección 28). FactorInteger encuentra los factores de un entero.
- RandomReal puede generar números con distribuciones diferentes de la uniforme. Por ejemplo, RandomReal[NormalDistribution[ ]] genera números con una distribución normal.
- Round redondea al entero más cercano (arriba o abajo); Floor siempre redondea hacia abajo; Ceiling siempre redondea hacia arriba.
- RealDigits es el análogo de IntegerDigits para números reales.