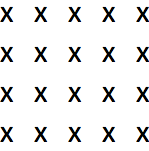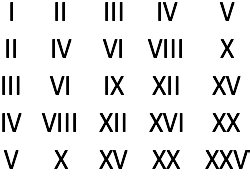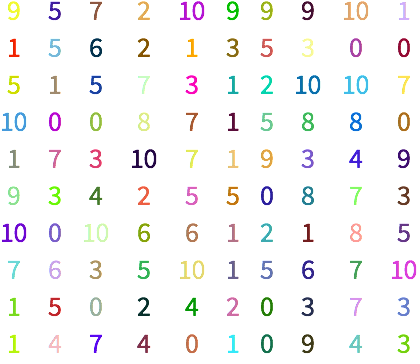WOLFRAM

An Elementary Introduction to the Wolfram Language
13Arreglos o listas de listas
Se ha visto anteriormente cómo utilizar Table para formar listas. Se verá ahora cómo se usa Table para crear arreglos de valores en un número mayor de dimensiones.
Haga una lista de 4 copias de x:
In[1]:=
Click for copyable input
Out[1]=
Haga una lista de 4 copias de una lista que contenga 5 copias de x:
In[2]:=
Click for copyable input
Out[2]=
Use Grid para presentar el resultado en una cuadrícula:
In[3]:=
Click for copyable input
Out[3]=
Puede usarse Table con dos variables para formar un arreglo en 2 dimensiones. La primera variable corresponde a la fila y, la segunda, a la columna.
Forme un arreglo de colores, con los rojos de arriba a abajo y los azules de izquierda a derecha:
In[4]:=
Click for copyable input
Out[4]=
Muestre un arreglo donde cada elemento corresponda con el número de la fila en que se encuentra:
In[5]:=
Click for copyable input
Out[5]=
Muestre un arreglo donde cada elemento corresponda con el número de la columna en que se encuentra:
In[6]:=
Click for copyable input
Out[6]=
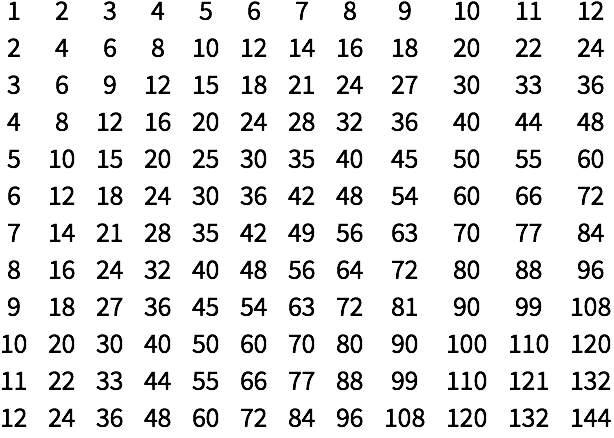
Genere un arreglo donde cada elemento sea la suma de los números de la fila y la columna en que se encuentre:
In[7]:=
Click for copyable input
Out[7]=
Genere una tabla de multiplicar:
In[8]:=
Click for copyable input
Out[8]=
ArrayPlot permite visualizar los valores en un arreglo. Mientras mayores sean los valores del arreglo, aparecerán con tonalidad más oscura.
Visualice una tabla de multiplicar:
In[9]:=
Click for copyable input
Out[9]=
Genere y grafique un arreglo de valores aleatorios:
In[10]:=
Click for copyable input
Out[10]=
ArrayPlot permite acomodar colores como si fueran valores:
In[11]:=
Click for copyable input
Out[11]=
En última instancia, las imágenes son arreglos de píxeles. En una imagen de color, un píxel contiene los valores del rojo, el verde y el azul. Cada píxel de una imagen en blanco y negro contiene los valores 0 (negro) o 1 (blanco). Pueden obtenerse los valores de cada píxel usando ImageData.
Encuentre los valores de los píxeles en la imagen de una “W”:
In[12]:=
Click for copyable input
Out[12]=
Este arreglo se visualiza usando ArrayPlot con los valores que contiene:
In[13]:=
Click for copyable input
Out[13]=
La imagen de arriba es de muy baja resolución porque, en este caso, así la generó Rasterize. Y, además, es blanco sobre negro en vez de negro sobre blanco, porque en una imagen el 0 equivale a negro y el 1 a blanco (como en color RGBColor), mientras que, por defecto, en ArrayPlot, mientras mayores sean los valores son también más oscuros.
Pueden hacerse operaciones aritméticas con arreglos, de la misma manera que con listas. Así pues, es sencillo intercambiar el 0 con el 1: simplemente cada valor se resta de 1, así que todos los 0 se cambian a 1−0=1, y todos los 1 se cambian a 1−1=0.
En este arreglo, se encuentran los valores de los píxeles y, luego, se utiliza una operación aritmética para intercambiar el 0 con el 1:
In[14]:=
Click for copyable input
Out[14]=
El resultado es negro sobre blanco:
In[15]:=
Click for copyable input
Out[15]=
Vocabulario
Table[x,4,5] hace un arreglo de valores en 2D
Grid[array] dispone los valores de un arreglo en una cuadrícula
ArrayPlot[array] visualiza los valores contenidos en un arreglo
ImageData[image] obtiene el arreglo que contenga los valores de los píxeles de una imagen
13.1Construya la tabla de multiplicar del 12. »
Salida esperada:
Out[]=
13.2Construya la tabla de multiplicar del 5 para números romanos. »
Salida esperada:
Out[]=
13.3Presente una cuadrícula de colores aleatorios de 10×10 . »
Muestra de salida esperada:
Out[]=
13.4Presente una cuadrícula de números enteros al azar, entre 0 y 10, con colores aleatorios entre 0 y 10. »
Muestra de salida esperada:
Out[]=
13.5Forme una cuadrícula con todas las cadenas posibles de pares de letras del alfabeto inglés (“aa”, “ab”, etc.). »
Salida esperada:
Out[]=
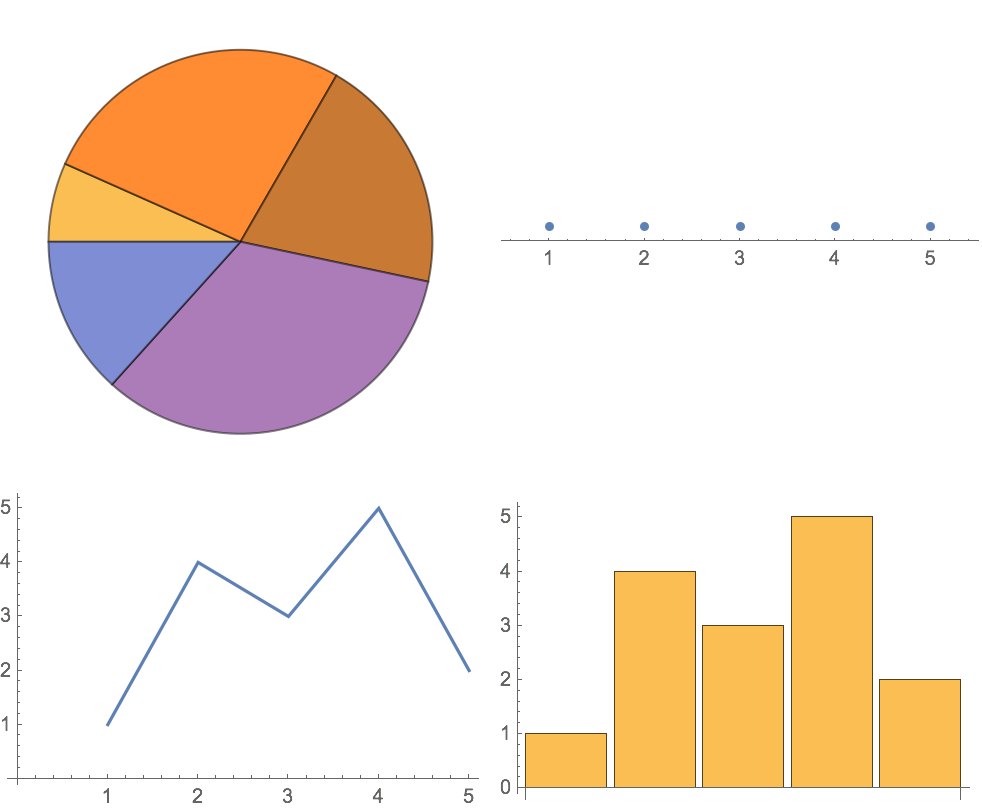
13.6Visualice {1, 4, 3, 5, 2} con un diagrama circular, con una recta numérica, con una gráfica de puntos unidos y con una gráfica de barras, colocando todas estas en una cuadrícula 2×2. »
Salida esperada:
Out[]=
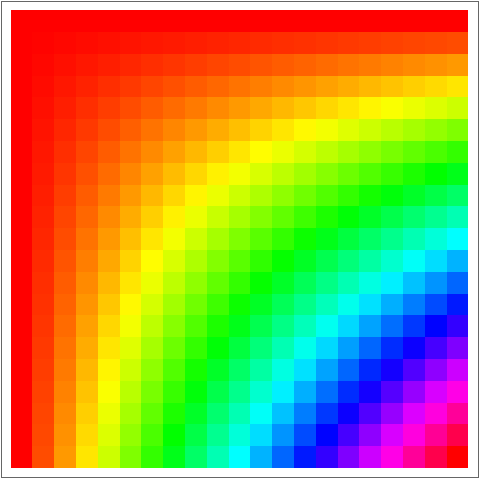
13.7Presente gráficamente el arreglo de las tonalidades con valores x*y, donde tanto x como y varíen entre 0 y 1, en incrementos de 0.05. »
Salida esperada:
Out[]=
13.8Presente gráficamente el arreglo de tonalidades x/y, donde tanto x como y varíen del 1 al 50 en incrementos de 1. »
Salida esperada:
Out[]=
Salida esperada:
Out[]=
+13.1Construya la tabla de sumar del 20. »
Salida esperada:
Out[]=
+13.2Forme una cuadrícula de 10×10 con enteros aleatorios entre 0 y 10, coloreados aleatoriamente y con tamaños aleatorios hasta 32. »
Muestra de salida esperada:
Out[]=
Preguntas y respuestas
¿Pueden depender uno de otro los límites de las variables en una tabla?
Sí; los últimos pueden depender de los primeros. Table[x, {i, 4}, {j, i}] forma un arreglo triangular “irregular”.
¿Pueden formarse tablas que sean listas de listas de listas?
Sí; pueden hacerse tablas de cualquier dimensión. Image3D es una manera de visualizar arreglos de dimensión 3.
En imágenes, ¿por qué el 0 corresponde al negro, y el 1 al blanco?
0 quiere decir intensidad cero de luz, es decir, negro. 1 quiere decir intensidad máxima, es decir, blanco.
¿Cómo se obtiene la imagen original a partir de la salida de ImageData?
Simplemente se le aplica la función Image.
Notas técnicas
 
Download Notebook Version
en